What Is 80 Of 35
salachar
Sep 07, 2025 · 5 min read
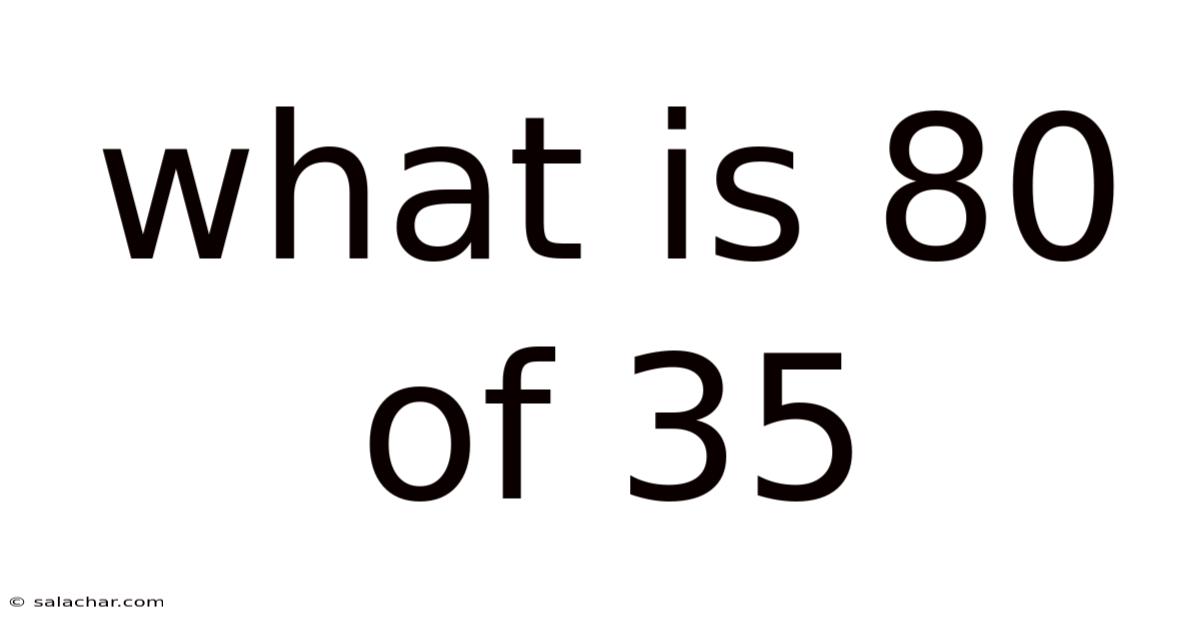
Table of Contents
What is 80% of 35? A Deep Dive into Percentages and Their Applications
Finding 80% of 35 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a vast world of applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial planning. This article will not only answer the question "What is 80% of 35?" but also explore the various methods for solving percentage problems, delve into the mathematical concepts behind them, and examine real-world examples to solidify your understanding.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 80% means 80 out of 100, which can be written as the fraction 80/100 or the decimal 0.8. This fundamental understanding is crucial for tackling percentage calculations.
Method 1: Converting Percentage to Decimal
The most straightforward way to find 80% of 35 is to convert the percentage to a decimal and then multiply.
-
Step 1: Convert the percentage to a decimal. To do this, divide the percentage by 100. So, 80% becomes 80 ÷ 100 = 0.8.
-
Step 2: Multiply the decimal by the number. Multiply the decimal (0.8) by the number you want to find the percentage of (35). This gives us 0.8 x 35 = 28.
Therefore, 80% of 35 is $\boxed{28}$.
Method 2: Using Fractions
Alternatively, you can solve this problem using fractions.
-
Step 1: Convert the percentage to a fraction. 80% can be written as the fraction 80/100. This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 20. This simplifies to 4/5.
-
Step 2: Multiply the fraction by the number. Multiply the simplified fraction (4/5) by 35: (4/5) x 35 = (4 x 35) / 5 = 140 / 5 = 28.
Again, we arrive at the answer: 80% of 35 is $\boxed{28}$.
Method 3: The Proportion Method
The proportion method offers a more visual and intuitive approach, particularly helpful for beginners. This method sets up a proportion, relating the percentage to the whole.
-
Step 1: Set up the proportion. We can set up a proportion as follows:
80/100 = x/35
Where 'x' represents the unknown value (80% of 35).
-
Step 2: Cross-multiply. Cross-multiply the terms to solve for x:
100x = 80 x 35
-
Step 3: Solve for x. Divide both sides by 100:
x = (80 x 35) / 100 = 2800 / 100 = 28
Therefore, 80% of 35 is $\boxed{28}$.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in many real-world scenarios. Here are a few examples:
-
Discounts: Imagine a store offering an 80% discount on a $35 item. Using the methods above, you would quickly determine the discount amount is $28, leaving you to pay only $7 ($35 - $28).
-
Taxes: Understanding percentages is crucial for calculating sales tax. If the sales tax is 8%, you would calculate 8% of the item's price to determine the tax amount.
-
Tips: Calculating tips in restaurants often involves percentages. A 20% tip on a $50 meal is easily calculated using the same principles.
-
Grade Calculations: Percentages are frequently used in academic settings to express grades and scores. A student scoring 80% on a 35-point test achieved 28 points.
-
Financial Planning: Percentages are fundamental to understanding interest rates, investment returns, and loan repayments. Calculating compound interest, for instance, relies heavily on percentage calculations.
-
Data Analysis: In statistics and data analysis, percentages are used extensively to represent proportions and probabilities within datasets. Understanding percentages allows for easier interpretation of survey results, market research data, and other statistical analyses.
Expanding Your Understanding: Beyond the Basics
While finding 80% of 35 is a relatively simple calculation, the underlying principles extend to more complex percentage problems. Consider these scenarios:
-
Finding the original value: If you know that 80% of a number is 28, you can use the same principles to find the original number. You would set up an equation: 0.8x = 28, and solve for x. This is an example of reverse percentage calculation.
-
Calculating percentage increase or decrease: Determining the percentage increase or decrease between two numbers involves finding the difference between the two numbers, dividing by the original number, and then multiplying by 100.
-
Compounding percentages: Compounding percentages occur when a percentage is applied repeatedly over time, such as with compound interest. These calculations require a slightly more advanced approach, often involving exponential growth equations.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest method depends on your preference and the complexity of the calculation. For simple calculations like finding 80% of 35, converting the percentage to a decimal and multiplying is generally the quickest. For more complex problems, the proportion method might offer a clearer approach.
Q2: Can I use a calculator for percentage calculations?
A2: Yes, most calculators have a percentage function (%) that simplifies these calculations. Simply enter the number, press the percentage button, and then multiply by the percentage you want to find.
Q3: Are there any online tools or resources for calculating percentages?
A3: Yes, many websites and apps offer online percentage calculators that can perform various percentage calculations, including finding percentages of numbers, calculating percentage increases or decreases, and more.
Q4: Why is it important to understand percentages?
A4: Understanding percentages is crucial for everyday life, from managing finances to interpreting data and making informed decisions in various aspects of life. It's a fundamental mathematical concept that underpins many real-world applications.
Conclusion
Finding 80% of 35, while a seemingly basic calculation, provides a gateway to understanding the broader world of percentages. This article has illustrated several methods for solving percentage problems, emphasized the importance of these calculations in diverse contexts, and encouraged a deeper exploration of the mathematical concepts behind them. Mastering percentages empowers you to navigate daily financial transactions, interpret data more effectively, and make better informed decisions in various aspects of your life. Remember to practice these methods regularly to strengthen your understanding and build confidence in tackling percentage problems of increasing complexity.
Latest Posts
Latest Posts
-
Monomers Of Dna And Rna
Sep 08, 2025
-
Lifting The Corporate Veil Meaning
Sep 08, 2025
-
The Madness Of Humpty Dumpty
Sep 08, 2025
-
Do Voltmeters Have High Resistance
Sep 08, 2025
-
Electronic Configuration Of Carbon Atom
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.