What Times What Equals 81
salachar
Aug 29, 2025 · 5 min read
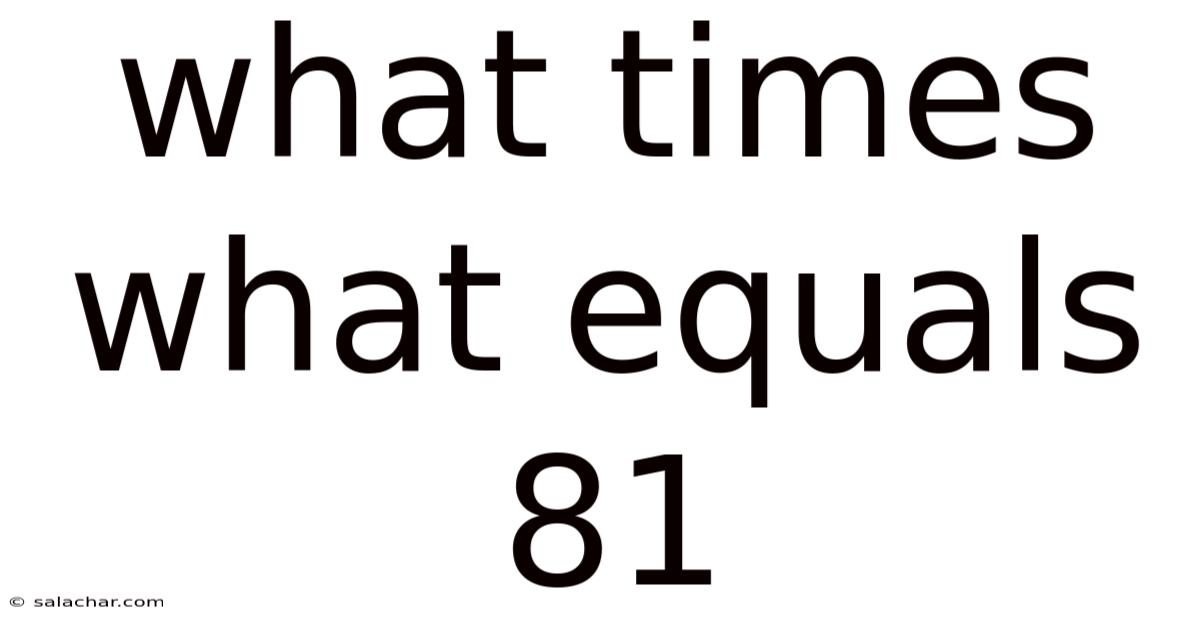
Table of Contents
What Times What Equals 81? Exploring Factors and Multiplication
Finding the numbers that multiply to equal 81 might seem like a simple arithmetic problem, but it opens a door to understanding fundamental concepts in mathematics, including factors, multiplication, prime factorization, and even the intriguing world of perfect squares. This article will delve into various ways to solve this seemingly straightforward question, exploring the underlying mathematical principles and expanding your understanding beyond just finding the answer. We'll also look at how this simple equation can relate to more complex mathematical concepts.
Understanding Factors and Multiplication
At its core, the question "What times what equals 81?" is asking for the factors of 81. Factors are whole numbers that divide evenly into another number without leaving a remainder. In simpler terms, they're the numbers you can multiply together to get a specific product. In this case, the product is 81.
Multiplication itself is a fundamental arithmetic operation representing repeated addition. When we say "x * y = 81," we're asking, "What number, when added to itself 'x' times, equals 81?" While this might not be the most efficient way to solve this particular problem, understanding this relationship helps grasp the underlying concept.
Finding the Factors of 81: A Systematic Approach
Let's systematically find all the factor pairs of 81. We'll start with the simplest factor pairs and work our way up:
-
1 x 81: This is the most obvious pair. Any number is divisible by 1 and itself.
-
3 x 27: We know 81 is divisible by 3 because the sum of its digits (8 + 1 = 9) is divisible by 3.
-
9 x 9: This is a special pair because it shows that 81 is a perfect square. A perfect square is a number that can be obtained by squaring another whole number (in this case, 9 x 9 = 9² = 81).
Therefore, the factor pairs of 81 are (1, 81), (3, 27), and (9, 9). These are all the whole number combinations that multiply to give 81.
Prime Factorization: Breaking it Down to the Basics
Prime factorization is a powerful technique for expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). Prime factorization helps us understand the building blocks of a number.
To find the prime factorization of 81, we can use a factor tree:
81
/ \
9 9
/ \ / \
3 3 3 3
This shows that the prime factorization of 81 is 3 x 3 x 3 x 3, or 3⁴. This means 81 is composed entirely of the prime number 3, multiplied by itself four times. This representation is unique to every number and is a fundamental concept in number theory.
Exploring Perfect Squares: The Significance of 81
As mentioned earlier, 81 is a perfect square (9²). This fact has several implications:
-
Geometric Representation: Imagine a square with sides of length 9 units. The area of this square is 9 * 9 = 81 square units. This geometric interpretation provides a visual understanding of the concept of a perfect square.
-
Square Roots: The square root of 81 (√81) is 9. This means that 9 multiplied by itself equals 81. The square root is the inverse operation of squaring.
-
Higher Powers: Because 81 is 9 squared, it can also be expressed as other powers. For example, it's 3 to the power of 4 (3⁴). This highlights the relationship between exponents and factors.
Beyond Whole Numbers: Considering Negative Factors
While the question focuses on whole numbers, it's important to consider that in mathematics, negative numbers also play a role. Since a negative number multiplied by a negative number results in a positive number, we can also say:
- -1 x -81 = 81
- -3 x -27 = 81
- -9 x -9 = 81
These factor pairs are equally valid solutions when expanding the scope beyond just positive whole numbers.
Extending the Concept: Applications in Algebra and Beyond
The simple equation "What times what equals 81?" lays the groundwork for more advanced mathematical concepts:
-
Solving Quadratic Equations: Quadratic equations often involve finding factors of a number to solve for the unknown variables. Understanding factoring is crucial for tackling such equations.
-
Number Theory: The concepts of factors, prime factorization, and perfect squares are fundamental building blocks in number theory, a branch of mathematics that explores the properties of numbers.
-
Algebraic Manipulation: The ability to identify factors is essential for simplifying and manipulating algebraic expressions.
Frequently Asked Questions (FAQ)
Q: Is there only one answer to "What times what equals 81?"
A: There are several answers depending on the context. If you restrict the solution to positive whole numbers, the answers are (1, 81), (3, 27), and (9,9). Including negative numbers expands the possibilities further.
Q: How can I quickly find the factors of a large number?
A: For larger numbers, systematically checking divisibility by prime numbers (2, 3, 5, 7, etc.) is a good strategy. Prime factorization techniques become increasingly important for larger numbers.
Q: What if the question was "What times what equals a different number?"
A: The same principles apply. Identify the factors of that number, employing prime factorization and considering both positive and negative factors as needed.
Q: What is the importance of understanding factors and multiplication?
A: Understanding factors and multiplication is essential for a strong foundation in mathematics. It's the basis for many more advanced concepts in algebra, calculus, and other fields.
Conclusion: More Than Just a Simple Equation
The seemingly simple question "What times what equals 81?" opens a window into the rich world of mathematics. Beyond finding the straightforward answers, understanding factors, prime factorization, perfect squares, and their applications in more complex mathematical concepts is crucial for building a strong mathematical foundation. This exploration illustrates how even the most fundamental mathematical concepts can lead to deeper understanding and appreciation of the beauty and logic inherent in mathematics. The ability to break down numbers into their components and manipulate them using the fundamental operations is a key skill for success in many mathematical and scientific fields.
Latest Posts
Latest Posts
-
1 Dozen Is How Many
Sep 01, 2025
-
Plastic Is Conductor Or Insulator
Sep 01, 2025
-
Definition Of Loading In Science
Sep 01, 2025
-
Duck Is Male Or Female
Sep 01, 2025
-
What Do Yorkshire Pigs Eat
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.