Whats 5 Percent Of 500
salachar
Sep 02, 2025 · 5 min read
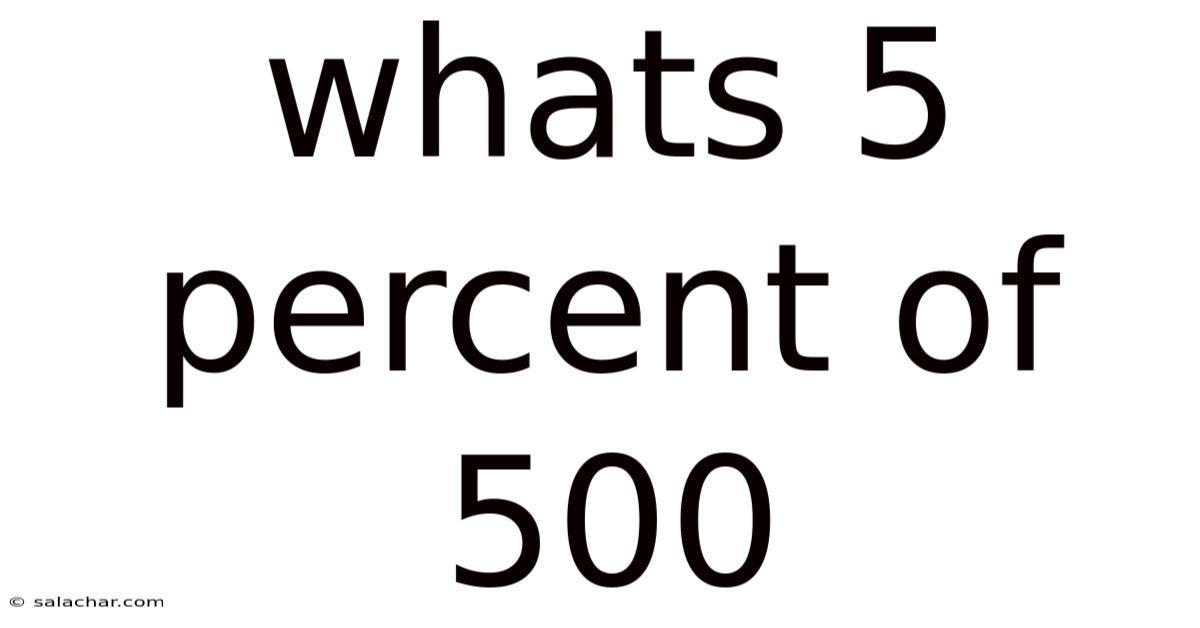
Table of Contents
What's 5 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 5 percent of 500 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for numerous applications in daily life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only answer the question "What's 5 percent of 500?" but also explore the broader concept of percentages, providing you with the tools to tackle similar problems confidently.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). It's a way to represent a portion of a whole. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Percentages are used extensively because they provide a standardized way to compare different quantities. Whether you're comparing test scores, market shares, or the growth of a company, percentages offer a clear and easily understandable comparison.
Calculating 5 Percent of 500: The Simple Method
The most straightforward way to calculate 5% of 500 is to convert the percentage to a decimal and then multiply:
-
Convert the percentage to a decimal: 5% is equivalent to 5/100 = 0.05.
-
Multiply the decimal by the number: 0.05 x 500 = 25
Therefore, 5 percent of 500 is $\boxed{25}$.
Alternative Methods for Calculating Percentages
While the above method is the most common and efficient for simple calculations, several alternative approaches can be helpful, especially when dealing with more complex scenarios:
-
Using fractions: 5% can be expressed as the fraction 5/100. To find 5% of 500, you can multiply 500 by 5/100: (5/100) x 500 = 25. This method is particularly useful when dealing with percentages that are easily expressed as simple fractions, such as 25%, 50%, or 75%.
-
Using proportions: You can set up a proportion to solve for the unknown value. The proportion would look like this: x/500 = 5/100. Cross-multiplying and solving for x gives you x = 25. This method is particularly helpful when dealing with more complex percentage problems where you need to solve for an unknown value within a proportion.
-
Using a calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 500 x 5 %, and the calculator will automatically perform the calculation and provide the answer: 25. This is the most convenient method for quick calculations.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous everyday situations, including:
-
Shopping and Sales: Calculating discounts and sales tax is a crucial skill for making informed purchasing decisions. For instance, if a $500 item is on sale for 20% off, you'd calculate the discount as 20% of $500 ($100), resulting in a final price of $400. Similarly, calculating sales tax (e.g., 6% of $400 = $24) adds to the final cost.
-
Finance and Investments: Percentages are fundamental to understanding interest rates, returns on investments, and financial statements. Calculating compound interest, for example, involves repeatedly applying percentage increases to a principal amount over time. This understanding allows for informed investment decisions and financial planning.
-
Science and Statistics: Percentages are used to represent data proportions in scientific studies, statistical analyses, and research reports. For example, calculating the percentage of participants in a study who responded positively to a treatment helps researchers draw meaningful conclusions.
-
Everyday Life: From calculating tips in restaurants (e.g., 15% of the bill) to understanding the percentage of ingredients in food products, percentages permeate various aspects of our daily routines.
Beyond the Basics: More Complex Percentage Problems
While finding 5% of 500 is a relatively simple calculation, the principles extend to more complex scenarios. Consider the following examples:
-
Finding the original amount: If you know that 5% of an unknown number is 25, you can use algebra to find the original number. Let x represent the original number: 0.05x = 25. Solving for x yields x = 500. This shows how you can work backward from a percentage and a resulting value to find the original amount.
-
Calculating percentage increase or decrease: Suppose a quantity increases from 500 to 525. To find the percentage increase, first calculate the difference (25), then divide by the original amount (500) and multiply by 100: (25/500) x 100 = 5%. Similarly, you can calculate percentage decreases.
-
Compounding percentages: This involves applying a percentage change repeatedly. For instance, if an investment of $500 grows by 5% annually for three years, the calculation becomes more intricate, requiring the application of the percentage increase for each year. This requires careful calculation using exponential growth or decay formulas.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate a percentage of a number without a calculator? A: You can use the methods described earlier: converting the percentage to a decimal and multiplying, using fractions, or setting up a proportion. Practice makes perfect!
-
Q: What if the percentage is a decimal, like 2.5%? A: Treat it the same way—convert the decimal percentage (2.5% = 0.025) and multiply by the number.
-
Q: Are there any online tools to calculate percentages? A: Yes, many websites and apps offer percentage calculators that can simplify the process.
Conclusion: Mastering Percentages for a Better Understanding of the World
Understanding percentages is a fundamental skill with far-reaching applications. While calculating 5% of 500 might seem trivial, the underlying principles extend to countless scenarios in everyday life, finance, science, and beyond. Mastering these principles allows for a deeper understanding of data, informed decision-making, and a more confident approach to problem-solving. From calculating discounts to interpreting statistical data, the ability to work with percentages empowers you to navigate the complexities of the world around you with greater clarity and precision. Remember to practice regularly and explore different methods to solidify your understanding. The more you practice, the more confident and efficient you will become in tackling percentage calculations of all kinds.
Latest Posts
Latest Posts
-
Difference Between Eagles And Hawks
Sep 02, 2025
-
Sex Linked Traits Punnett Square
Sep 02, 2025
-
Computers In Biology And Medicine
Sep 02, 2025
-
John Cena Osama Bin Laden
Sep 02, 2025
-
Is 997 A Prime Number
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about Whats 5 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.