Why Is Cos 0 1
salachar
Sep 12, 2025 · 5 min read
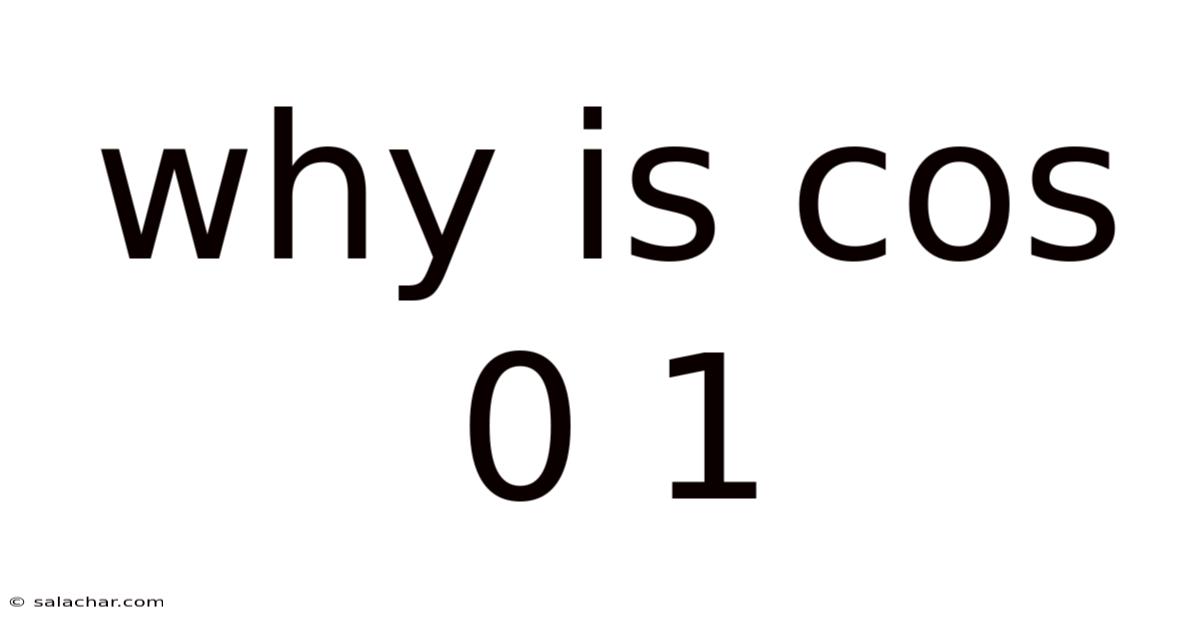
Table of Contents
Why is cos 0 = 1? Unraveling the Mystery of the Cosine Function
The question, "Why is cos 0 = 1?" might seem simple at first glance, especially for those familiar with trigonometry. However, a truly satisfying answer requires delving into the fundamental definitions of cosine, its relationship to the unit circle, and its broader applications in mathematics and beyond. This article will explore these aspects, providing a comprehensive explanation accessible to both beginners and those seeking a deeper understanding. We'll move beyond a simple statement of fact and uncover the why behind this crucial trigonometric identity.
Understanding the Unit Circle
The core to understanding why cos 0 = 1 lies in visualizing the unit circle. The unit circle is a circle with a radius of 1, centered at the origin (0, 0) of a coordinate plane. This seemingly simple geometric construct is the foundation for understanding trigonometric functions like sine and cosine.
Imagine a point on the unit circle. The angle θ (theta) is measured counter-clockwise from the positive x-axis to the line segment connecting the origin to that point. The cosine of this angle (cos θ) is defined as the x-coordinate of that point. The sine of the angle (sin θ) is defined as the y-coordinate.
Now, let's consider the case where θ = 0. When the angle is 0, the line segment connecting the origin to the point on the unit circle lies entirely along the positive x-axis. The point's coordinates are therefore (1, 0). Since the cosine is the x-coordinate, cos 0 = 1.
Visualizing the Relationship: A Geometric Perspective
Think of a right-angled triangle. The cosine of an angle in this triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. As the angle approaches 0, the adjacent side becomes increasingly closer in length to the hypotenuse.
Imagine shrinking the angle until it's practically nonexistent. The adjacent side and hypotenuse become virtually indistinguishable, their lengths approaching equality. This ratio, adjacent/hypotenuse, approaches 1. Therefore, as the angle approaches 0, the cosine of the angle approaches 1. At exactly 0 degrees, the ratio is precisely 1, leading to cos 0 = 1.
The Power Series Expansion: A Deeper Dive
A more rigorous mathematical explanation involves the power series expansion of the cosine function. This expansion represents the cosine function as an infinite sum of terms:
cos x = 1 - x²/2! + x⁴/4! - x⁶/6! + ...
where x is the angle in radians, and n! denotes the factorial of n (e.g., 3! = 3 × 2 × 1 = 6).
When x = 0, all terms except the first become 0. This leaves us with:
cos 0 = 1
This confirms our previous geometric intuition through a more formal mathematical approach. The power series provides a powerful analytical tool for understanding the behavior of trigonometric functions.
Connecting Cosine to Other Trigonometric Identities
The identity cos 0 = 1 is crucial for establishing numerous other trigonometric identities. For example:
-
Cosine of Negative Angles: cos(-x) = cos(x). This implies cos(0) = cos(-0) = 1.
-
Pythagorean Identity: sin²x + cos²x = 1. If x = 0, we have sin²(0) + cos²(0) = 1. Since sin(0) = 0, this equation directly confirms cos(0) = 1.
-
Double Angle Formula: cos(2x) = cos²(x) - sin²(x). When x = 0, this simplifies to cos(0) = cos²(0) - sin²(0) = 1 - 0 = 1.
These identities, built upon the foundation of cos 0 = 1, underpin a wide array of applications in various fields.
Applications of Cosine and its Identity
The cosine function, and the identity cos 0 = 1, are foundational in numerous areas:
-
Physics: Cosine is essential in describing oscillatory motion (like simple harmonic motion), wave propagation, and the resolution of vectors into components. The initial conditions in many physical problems often rely on the cosine function evaluated at 0.
-
Engineering: Cosine plays a critical role in signal processing, circuit analysis, and mechanical engineering, particularly in dealing with rotating systems.
-
Computer Graphics and Game Development: Cosine is used extensively in 3D graphics to perform rotations, transformations, and calculations related to angles and positions in space.
-
Navigation and Surveying: Cosine is crucial in calculations involving distances, bearings, and angles used in GPS, surveying, and other location-based technologies.
Frequently Asked Questions (FAQs)
Q1: Why is the cosine function important?
A1: The cosine function is fundamental because it describes periodic behavior and relationships between angles and lengths. Its applications span numerous fields, making it a cornerstone of mathematics and science.
Q2: Are there other angles where the cosine is 1?
A2: Yes, the cosine function is periodic, with a period of 2π radians (or 360 degrees). This means cos(2πk) = 1 for any integer k. Cosine is also 1 at multiples of 360 degrees.
Q3: How can I remember the value of cos 0?
A3: Visualizing the unit circle is the most effective method. When the angle is 0, the point on the unit circle lies on the positive x-axis, where the x-coordinate is 1.
Q4: What about the cosine of other angles?
A4: The cosine of other angles can be determined using various methods including the unit circle, right-angled triangles, power series expansions, or trigonometric identities. The values for common angles are often memorized or easily calculated.
Q5: Can cos 0 = 1 be proven without using the unit circle?
A5: Yes, the power series expansion of the cosine function provides a rigorous algebraic proof independent of geometric visualization.
Conclusion
The seemingly straightforward identity cos 0 = 1 is far more significant than it first appears. It stems from the very definition of the cosine function, whether viewed geometrically through the unit circle or analytically through its power series expansion. This identity is the bedrock for a vast number of other trigonometric identities and plays an essential role in numerous scientific and engineering applications. Understanding why cos 0 = 1 not only reinforces a fundamental trigonometric concept but also reveals the elegant interconnectedness of mathematics and its far-reaching implications in the real world. The journey to understanding this simple yet profound identity underscores the power of mathematical reasoning and the beauty of its applications.
Latest Posts
Latest Posts
-
What Is Half Of 2000
Sep 12, 2025
-
Factors Of 98 In Pairs
Sep 12, 2025
-
Is Yeast Eukaryotic Or Prokaryotic
Sep 12, 2025
-
Diagram Of Ceiling Fan Parts
Sep 12, 2025
-
Chemical To Thermal Electrical Current
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Why Is Cos 0 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.