X 2 12x 36 Factor
salachar
Sep 10, 2025 · 6 min read
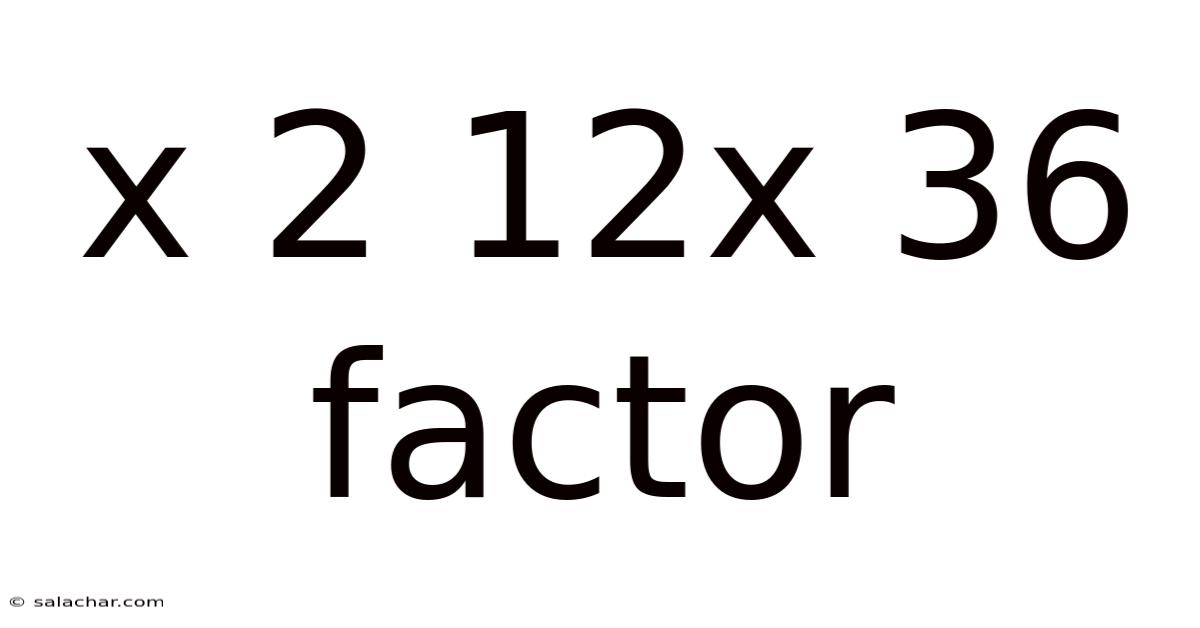
Table of Contents
Decoding the Factorization of x² + 12x + 36: A Comprehensive Guide
Understanding quadratic expressions and their factorization is fundamental to success in algebra. This article delves into the factorization of the quadratic expression x² + 12x + 36, explaining the process step-by-step, exploring the underlying mathematical principles, and answering frequently asked questions. This comprehensive guide aims to equip you with the knowledge and skills to tackle similar problems confidently. We will explore various methods, ensuring you grasp the concepts thoroughly. Mastering this will lay a strong foundation for more advanced algebraic concepts.
Understanding Quadratic Expressions
Before diving into the factorization of x² + 12x + 36, let's establish a basic understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our target expression, x² + 12x + 36, fits this form perfectly, with a = 1, b = 12, and c = 36.
Method 1: Factoring by Finding Two Numbers
This is a common and often the most efficient method for factoring simple quadratic expressions. The goal is to find two numbers that add up to 'b' (the coefficient of x) and multiply to 'c' (the constant term).
In our expression, x² + 12x + 36:
- b = 12
- c = 36
We need to find two numbers that add up to 12 and multiply to 36. Let's brainstorm:
- 1 + 35 = 36 (but 1 * 35 ≠ 36)
- 2 + 18 = 20 (but 2 * 18 ≠ 36)
- 3 + 12 = 15 (but 3 * 12 ≠ 36)
- 4 + 9 = 13 (but 4 * 9 ≠ 36)
- 6 + 6 = 12 (and 6 * 6 = 36)
We found our numbers! Both are 6.
Now, we can rewrite the expression:
x² + 6x + 6x + 36
Next, we factor by grouping:
x(x + 6) + 6(x + 6)
Notice that (x + 6) is a common factor. We can factor it out:
(x + 6)(x + 6)
Therefore, the factorization of x² + 12x + 36 is (x + 6)². This is also known as a perfect square trinomial.
Method 2: Using the Quadratic Formula
While the previous method is efficient for simpler quadratics, the quadratic formula provides a more general approach that works for all quadratic equations, even those that are not easily factorable by inspection. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression, x² + 12x + 36, a = 1, b = 12, and c = 36. Substituting these values into the quadratic formula:
x = [-12 ± √(12² - 4 * 1 * 36)] / (2 * 1) x = [-12 ± √(144 - 144)] / 2 x = [-12 ± √0] / 2 x = -12 / 2 x = -6
Since the discriminant (b² - 4ac) is 0, we have a repeated root, x = -6. This means the factored form is (x - (-6))(x - (-6)) which simplifies to (x + 6)(x + 6) or (x + 6)². This confirms our result from Method 1.
Method 3: Recognizing a Perfect Square Trinomial
A perfect square trinomial is a quadratic expression that can be factored into the square of a binomial. It has the form a² + 2ab + b² = (a + b)². Our expression, x² + 12x + 36, fits this pattern:
- x² is the square of x (a = x)
- 36 is the square of 6 (b = 6)
- 12x is twice the product of x and 6 (2ab = 2 * x * 6 = 12x)
Therefore, we can directly factor it as (x + 6)². Recognizing this pattern significantly shortens the factorization process.
The Significance of Factoring
Factoring quadratic expressions is more than just an algebraic exercise. It's a crucial skill with numerous applications:
-
Solving Quadratic Equations: Factoring allows us to solve quadratic equations by setting each factor equal to zero. For example, to solve x² + 12x + 36 = 0, we would set (x + 6)² = 0, leading to x = -6.
-
Simplifying Algebraic Expressions: Factoring can simplify complex expressions, making them easier to manipulate and analyze.
-
Graphing Parabolas: The factored form of a quadratic expression reveals the x-intercepts (roots) of the corresponding parabola, providing valuable information for graphing. In our case, the parabola y = x² + 12x + 36 touches the x-axis only at x = -6.
-
Calculus and Beyond: Factoring plays a significant role in calculus and other advanced mathematical fields. Techniques like partial fraction decomposition rely heavily on factorization skills.
Scientific Explanation: Connecting to Geometry
The factorization of x² + 12x + 36 has a visual representation in geometry. Consider a square with sides of length 'x' and a rectangle with sides of length 'x' and 6. Adding these together, we have an area represented by x² + 6x. However, this isn't a complete square. To make it a complete square, we need to add another square with sides of length 6, which has an area of 36. The total area becomes x² + 6x + 36, which is a perfect square with side length x+6. This perfectly illustrates the factorization (x+6)².
Frequently Asked Questions (FAQs)
Q1: What if the quadratic expression cannot be factored easily?
A1: If the quadratic expression cannot be easily factored using the methods described above, you can use the quadratic formula to find the roots. The roots can then be used to write the factored form. Alternatively, numerical methods can be employed to approximate the roots.
Q2: Are there other types of quadratic expressions?
A2: Yes, there are different types of quadratic expressions. Some have distinct roots, while others have repeated roots (as seen in our example). Some have no real roots but complex roots. Understanding these variations is crucial for solving various problems.
Q3: What is the importance of the discriminant (b² - 4ac)?
A3: The discriminant helps determine the nature of the roots of a quadratic equation. * If b² - 4ac > 0, there are two distinct real roots. * If b² - 4ac = 0, there is one repeated real root (as in our example). * If b² - 4ac < 0, there are two complex roots.
Q4: Can I use this method for other quadratic expressions?
A4: Absolutely! These methods, especially finding two numbers that add to 'b' and multiply to 'c' and recognizing perfect square trinomials, are applicable to many other quadratic expressions. However, remember that not all quadratic expressions can be factored easily using integers.
Conclusion
Factoring the quadratic expression x² + 12x + 36 into (x + 6)² is a straightforward process once you understand the underlying principles. Whether you employ the method of finding two numbers, the quadratic formula, or recognize the perfect square trinomial pattern, the key is to develop a strong understanding of the concepts and practice regularly. This mastery is not just about solving a single problem; it builds a solid foundation for tackling more complex algebraic concepts in the future and opens doors to advanced applications in mathematics and other related fields. Remember to practice regularly to solidify your understanding and build confidence in your ability to tackle similar problems efficiently and accurately.
Latest Posts
Latest Posts
-
What Are Factors For 33
Sep 10, 2025
-
Snake And Mongoose Hot Wheels
Sep 10, 2025
-
White And Brown Hunting Dog
Sep 10, 2025
-
Portrait Of A Woman Book
Sep 10, 2025
-
Difference Between Dissociation And Ionisation
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X 2 12x 36 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.