X 2 6x 27 0
salachar
Sep 11, 2025 · 6 min read
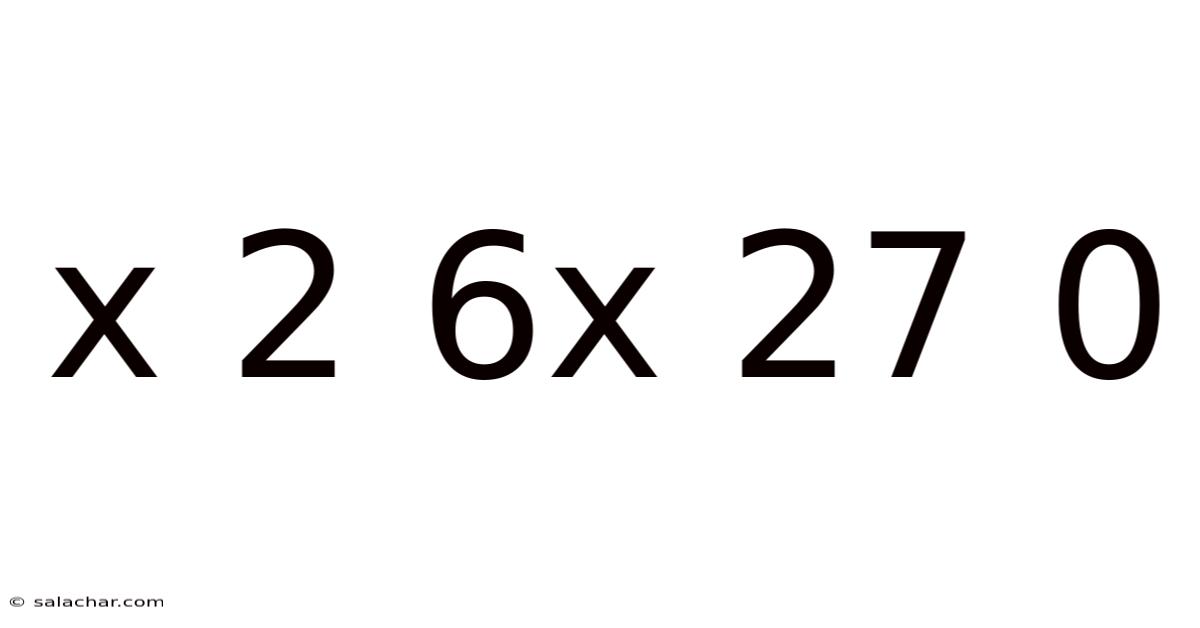
Table of Contents
Decoding the Mystery: A Deep Dive into the Equation x² + 6x + 27 = 0
This article explores the quadratic equation x² + 6x + 27 = 0, examining its solutions, the methods used to solve it, and the broader mathematical concepts it exemplifies. We'll delve into the different approaches to solving quadratic equations, highlighting the importance of understanding the underlying principles rather than just memorizing formulas. This exploration will be beneficial for students learning about quadratic equations, as well as anyone interested in refreshing their knowledge of fundamental algebra. Understanding quadratic equations is crucial in various fields, from physics and engineering to finance and computer science.
Introduction to Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a is not equal to zero. Our specific equation, x² + 6x + 27 = 0, fits this general form with a = 1, b = 6, and c = 27.
Solving a quadratic equation means finding the values of x that make the equation true. There are several methods to achieve this, each with its strengths and weaknesses. Let's explore the most common techniques and apply them to our equation.
Method 1: Factoring
Factoring involves expressing the quadratic expression as a product of two linear expressions. This method is efficient when the quadratic expression can be easily factored. Unfortunately, not all quadratic equations are easily factorable. Let's attempt factoring x² + 6x + 27 = 0:
We look for two numbers that add up to 6 (the coefficient of x) and multiply to 27 (the constant term). There are no two real numbers that satisfy this condition. The factors of 27 are 1 and 27, 3 and 9, and their negative counterparts. None of these pairs add up to 6. Therefore, this equation cannot be solved by simple factoring using real numbers.
Method 2: Quadratic Formula
The quadratic formula is a powerful tool that provides the solutions for any quadratic equation, regardless of whether it's easily factorable. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply this formula to our equation x² + 6x + 27 = 0, where a = 1, b = 6, and c = 27:
x = [-6 ± √(6² - 4 * 1 * 27)] / (2 * 1) x = [-6 ± √(36 - 108)] / 2 x = [-6 ± √(-72)] / 2
Notice that we have a negative number under the square root. This indicates that the solutions are complex numbers, involving the imaginary unit i, where i² = -1.
Understanding Complex Numbers
Complex numbers are numbers of the form a + bi, where a and b are real numbers, and i is the imaginary unit. In our case, we have √(-72) which can be simplified as follows:
√(-72) = √(36 * -2) = √36 * √-2 = 6√2i
Therefore, the solutions to our quadratic equation are:
x = [-6 + 6√2i] / 2 = -3 + 3√2i x = [-6 - 6√2i] / 2 = -3 - 3√2i
These are two distinct complex conjugate solutions. Complex conjugate pairs always arise when solving quadratic equations with real coefficients that have a negative discriminant (the expression inside the square root in the quadratic formula, b² - 4ac).
Method 3: Completing the Square
Completing the square is another method for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. While the quadratic formula is often quicker, completing the square offers valuable insight into the structure of quadratic equations.
Let's complete the square for x² + 6x + 27 = 0:
- Move the constant term to the right side: x² + 6x = -27
- Take half of the coefficient of x (6/2 = 3), square it (3² = 9), and add it to both sides: x² + 6x + 9 = -27 + 9
- Factor the left side as a perfect square: (x + 3)² = -18
- Take the square root of both sides: x + 3 = ±√(-18) = ±3√2i
- Solve for x: x = -3 ± 3√2i
This confirms the solutions we obtained using the quadratic formula.
The Discriminant and the Nature of Roots
The discriminant (b² - 4ac) is a crucial part of the quadratic formula. It determines the nature of the roots (solutions) of the quadratic equation:
- Positive Discriminant: Two distinct real roots.
- Zero Discriminant: One real root (a repeated root).
- Negative Discriminant: Two distinct complex conjugate roots.
In our case, the discriminant is 36 - 108 = -72, which is negative. This confirms the presence of two distinct complex conjugate roots, as we've found.
Graphical Representation
Graphically, a quadratic equation represents a parabola. The x-intercepts of the parabola represent the real roots of the equation. Since our equation has complex roots, its parabola does not intersect the x-axis. The parabola opens upwards (since a = 1 > 0) and lies entirely above the x-axis.
Applications of Quadratic Equations
Quadratic equations are not just abstract mathematical concepts; they have widespread applications in various fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing bridges, buildings, and other structures. Analyzing stress and strain in materials.
- Finance: Modeling investment growth, calculating compound interest, and determining break-even points in business.
- Computer Science: Used in algorithms and computer graphics.
Frequently Asked Questions (FAQ)
Q: Why are complex numbers important?
A: Complex numbers extend the number system beyond real numbers, allowing us to solve equations that have no real solutions. They have numerous applications in various fields, including electrical engineering, quantum mechanics, and signal processing.
Q: Can a quadratic equation have only one solution?
A: Yes, if the discriminant (b² - 4ac) is equal to zero, the quadratic equation has one real root (a repeated root).
Q: Is there a method to solve quadratic equations without using the quadratic formula?
A: Yes, factoring and completing the square are alternative methods, although the quadratic formula is generally more efficient and applicable to all cases.
Q: What if 'a' in the quadratic equation is zero?
A: If a is zero, the equation is no longer quadratic; it becomes a linear equation, which is easily solved.
Conclusion
The equation x² + 6x + 27 = 0, while seemingly simple, provides a valuable opportunity to explore the richness of quadratic equations and the broader world of complex numbers. Understanding the various methods of solving quadratic equations, along with the significance of the discriminant, is crucial for success in algebra and its diverse applications. Remember, the key is not just memorizing formulas but understanding the underlying principles and their implications. This deep dive into the seemingly simple equation has revealed the complexity and beauty hidden within the world of mathematics. The journey from a simple equation to the realm of complex numbers highlights the power and elegance of mathematical problem-solving.
Latest Posts
Latest Posts
-
Definition Of Mode In Psychology
Sep 11, 2025
-
Where To Purchase Grain Alcohol
Sep 11, 2025
-
Nitric Acid Reacts With Copper
Sep 11, 2025
-
Is Cfcs A Greenhouse Gas
Sep 11, 2025
-
Difference Between Detergent And Soap
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about X 2 6x 27 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.