Y 2x X 2 Graph
salachar
Sep 12, 2025 · 6 min read
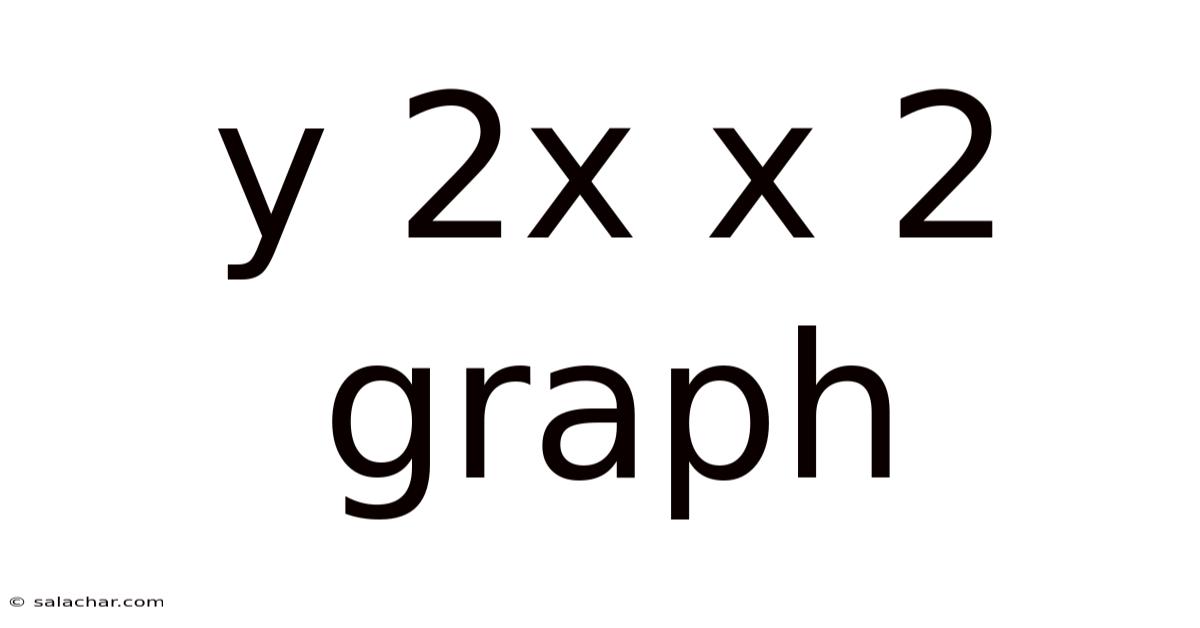
Table of Contents
Unveiling the Secrets of the y = 2x² + x - 2 Graph: A Comprehensive Guide
Understanding quadratic functions is fundamental to mastering algebra and calculus. This comprehensive guide delves into the intricacies of the quadratic function represented by the equation y = 2x² + x - 2, exploring its properties, graphical representation, and practical applications. We will cover key aspects such as finding the vertex, intercepts, axis of symmetry, and using this knowledge to sketch an accurate and insightful graph. By the end, you'll not only be able to graph this specific equation but also possess the tools to analyze any quadratic function effectively.
I. Introduction: Understanding Quadratic Functions
A quadratic function is a polynomial function of degree two, meaning the highest power of the variable (x in this case) is 2. It generally takes the form y = ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The graph of a quadratic function is always a parabola – a symmetrical U-shaped curve. The value of 'a' determines whether the parabola opens upwards (a > 0) or downwards (a < 0). In our equation, y = 2x² + x - 2, a = 2, b = 1, and c = -2. Since 'a' (2) is positive, the parabola opens upwards.
II. Finding the Vertex: The Turning Point of the Parabola
The vertex is the lowest (or highest, if the parabola opens downwards) point on the parabola. It represents the minimum (or maximum) value of the function. The x-coordinate of the vertex can be found using the formula x = -b / 2a. In our case:
x = -1 / (2 * 2) = -1/4
Now, substitute this x-value back into the original equation to find the corresponding y-coordinate:
y = 2(-1/4)² + (-1/4) - 2 = 2(1/16) - 1/4 - 2 = 1/8 - 1/4 - 2 = -17/8
Therefore, the vertex of the parabola is (-1/4, -17/8).
III. Determining the x-intercepts: Where the Graph Crosses the x-axis
The x-intercepts are the points where the graph intersects the x-axis, meaning the y-coordinate is zero. To find them, we set y = 0 and solve the quadratic equation:
2x² + x - 2 = 0
This quadratic equation doesn't factor easily, so we'll use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 2, b = 1, c = -2):
x = [-1 ± √(1² - 4 * 2 * -2)] / (2 * 2) = [-1 ± √17] / 4
This gives us two x-intercepts:
x₁ = (-1 + √17) / 4 ≈ 0.78 x₂ = (-1 - √17) / 4 ≈ -1.28
Therefore, the x-intercepts are approximately (0.78, 0) and (-1.28, 0).
IV. Finding the y-intercept: Where the Graph Crosses the y-axis
The y-intercept is the point where the graph intersects the y-axis, meaning the x-coordinate is zero. To find it, we simply substitute x = 0 into the original equation:
y = 2(0)² + (0) - 2 = -2
Therefore, the y-intercept is (0, -2).
V. Identifying the Axis of Symmetry: The Line of Reflection
The axis of symmetry is a vertical line that divides the parabola into two mirror images. Its equation is given by x = -b / 2a, which is the same as the x-coordinate of the vertex. In our case, the axis of symmetry is x = -1/4.
VI. Sketching the Graph: Bringing it All Together
Now that we have the vertex, x-intercepts, y-intercept, and axis of symmetry, we can sketch the graph.
- Plot the vertex: (-1/4, -17/8)
- Plot the intercepts: (0.78, 0), (-1.28, 0), and (0, -2)
- Draw the axis of symmetry: x = -1/4
- Sketch the parabola: Remember it opens upwards since a > 0. The parabola should be symmetrical about the axis of symmetry. Use the plotted points as guides to create a smooth, U-shaped curve.
Remember that the accuracy of your sketch depends on how precisely you plot the points. You may want to use graph paper for better accuracy.
VII. Further Analysis: Exploring the Properties of the Parabola
Beyond the basic characteristics already explored, further analysis can reveal more nuanced properties of the y = 2x² + x - 2 graph.
-
Range: Since the parabola opens upwards, the range represents all y-values greater than or equal to the y-coordinate of the vertex. Therefore, the range is [-17/8, ∞).
-
Domain: The domain of a quadratic function is always all real numbers, denoted as (-∞, ∞). This means the function is defined for all possible x-values.
-
Increasing and Decreasing Intervals: The function is decreasing for x-values less than -1/4 and increasing for x-values greater than -1/4.
-
Concavity: The parabola is concave up, meaning it curves upwards. This is indicated by the positive value of 'a' (a = 2).
-
End Behavior: As x approaches positive or negative infinity, the y-values approach positive infinity. This is characteristic of parabolas that open upwards.
VIII. Applications of Quadratic Functions: Real-World Connections
Quadratic functions are not merely abstract mathematical concepts; they have numerous practical applications in various fields. Some examples include:
-
Projectile Motion: The trajectory of a projectile (e.g., a ball thrown into the air) can be modeled using a quadratic function. The function describes the height of the projectile as a function of time.
-
Optimization Problems: Quadratic functions are often used to find maximum or minimum values in optimization problems. For example, finding the dimensions of a rectangle with a fixed perimeter that maximizes its area.
-
Engineering and Physics: Quadratic functions appear in numerous engineering and physics applications, including the study of oscillations, vibrations, and the design of parabolic reflectors.
-
Economics: Quadratic functions can model various economic phenomena, such as cost functions, revenue functions, and profit functions.
IX. Frequently Asked Questions (FAQ)
Q1: How can I find the roots of the quadratic equation 2x² + x - 2 = 0 without using the quadratic formula?
A1: While the quadratic formula is the most reliable method for solving any quadratic equation, you can attempt to factor the equation. However, in this case, the equation doesn't factor neatly using integer coefficients. The quadratic formula provides the most accurate and efficient solution.
Q2: What if the parabola opened downwards? How would that change the analysis?
A2: If the parabola opened downwards (a < 0), the vertex would represent the maximum value of the function. The range would be (-∞, y-coordinate of the vertex], and the concavity would be concave down. The process of finding the intercepts and axis of symmetry remains the same.
Q3: Can I use software or a graphing calculator to graph this function?
A3: Absolutely! Software like GeoGebra, Desmos, or graphing calculators can easily graph quadratic functions. Inputting the equation y = 2x² + x - 2 will generate a precise graph, allowing you to verify your hand-drawn sketch.
X. Conclusion: Mastering Quadratic Functions
This detailed exploration of the graph y = 2x² + x - 2 has provided a comprehensive understanding of quadratic functions, demonstrating the steps involved in analyzing and graphing these important mathematical objects. By understanding the concepts of the vertex, intercepts, axis of symmetry, and other properties, you have gained valuable skills applicable not only to graphing but also to solving various real-world problems. Remember, the key to mastering quadratic functions lies in understanding the underlying principles and applying them systematically. Through practice and continued learning, you can confidently tackle more complex quadratic functions and appreciate their significant role in mathematics and various applied fields.
Latest Posts
Latest Posts
-
Fox And The Hen House
Sep 12, 2025
-
Good Words To Describe Mom
Sep 12, 2025
-
Difference Between Cardinal And Ordinal
Sep 12, 2025
-
How Does An Atomizer Work
Sep 12, 2025
-
We The People Chapter 4 8
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Y 2x X 2 Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.