3 40 As A Percent
salachar
Sep 13, 2025 · 5 min read
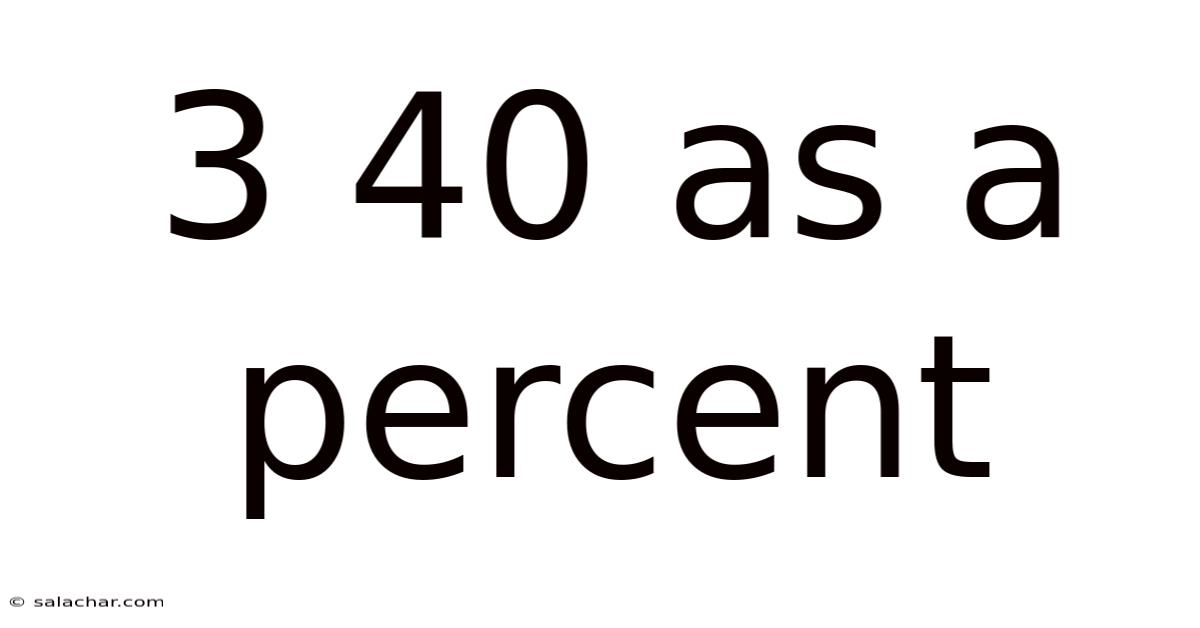
Table of Contents
Understanding 3/40 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from everyday finances to advanced scientific calculations. This comprehensive guide will walk you through the process of converting the fraction 3/40 into a percentage, exploring different methods, explaining the underlying concepts, and providing practical examples to solidify your understanding. We'll also delve into the broader context of fraction-to-percentage conversions and address frequently asked questions.
Understanding Fractions and Percentages
Before diving into the conversion of 3/40, let's briefly review the core concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/40, 3 is the numerator and 40 is the denominator.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of a hundred. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2.
Method 1: Converting the Fraction Directly to a Percentage
The most straightforward method for converting 3/40 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (40). 3 ÷ 40 = 0.075
-
Multiply the decimal by 100: This converts the decimal to a percentage. 0.075 × 100 = 7.5%
Therefore, 3/40 is equal to 7.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This directly gives us the percentage since percentages are based on a denominator of 100.
To achieve this, we need to determine what number we need to multiply the denominator (40) by to get 100. This is found by dividing 100 by 40:
100 ÷ 40 = 2.5
Now, we multiply both the numerator and the denominator of the original fraction (3/40) by 2.5:
(3 × 2.5) / (40 × 2.5) = 7.5 / 100
Since the denominator is now 100, the numerator directly represents the percentage: 7.5%.
Method 3: Using Proportions
A more formal approach uses the concept of proportions. We can set up a proportion to solve for the percentage:
3/40 = x/100
Here, 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
40x = 300
Now, divide both sides by 40:
x = 300 ÷ 40 = 7.5
Therefore, x = 7.5%.
Practical Applications and Real-World Examples
Understanding how to convert fractions to percentages is crucial in many real-world situations:
-
Finance: Calculating interest rates, discounts, tax percentages, and profit margins often involves converting fractions to percentages. For example, if a store offers a discount of 3/40 on an item, it means a 7.5% discount.
-
Statistics: Percentages are frequently used to represent data and probabilities. For instance, if 3 out of 40 students in a class passed an exam with distinction, it means 7.5% of the students achieved distinction.
-
Science: Percentages are used to express concentrations, efficiencies, and error margins in scientific experiments and research.
-
Everyday Life: We encounter percentages in various daily situations, such as calculating tips, understanding sale prices, or interpreting survey results.
Further Exploration: Working with Different Fractions
Let's extend our understanding by looking at how to convert other fractions to percentages. The methods outlined above remain consistent:
-
1/4: 1 ÷ 4 = 0.25; 0.25 × 100 = 25%
-
7/20: 7 ÷ 20 = 0.35; 0.35 × 100 = 35%
-
5/8: 5 ÷ 8 = 0.625; 0.625 × 100 = 62.5%
-
11/50: 11 ÷ 50 = 0.22; 0.22 × 100 = 22%
These examples illustrate the versatility of the conversion methods, allowing you to tackle various fractional values confidently. The key is always to divide the numerator by the denominator and then multiply the resulting decimal by 100.
Common Mistakes to Avoid
While the process is straightforward, some common mistakes can lead to incorrect results:
-
Incorrect order of operations: Always perform the division (numerator ÷ denominator) before multiplying by 100.
-
Misplacing the decimal point: Pay close attention to the placement of the decimal point during the decimal-to-percentage conversion.
-
Rounding errors: When dealing with recurring decimals, be mindful of rounding appropriately based on the context and required level of precision.
Frequently Asked Questions (FAQ)
Q: Can I convert percentages back to fractions?
A: Yes, absolutely. To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 7.5% becomes 7.5/100, which simplifies to 3/40.
Q: What if the fraction is an improper fraction (where the numerator is larger than the denominator)?
A: You can still use the same methods. Convert the improper fraction to a mixed number (a whole number and a proper fraction), then convert the fractional part to a percentage and add it to the whole number. Alternatively, you can directly divide the numerator by the denominator, and then multiply by 100. For example, 5/2 = 2.5; 2.5 * 100 = 250%.
Q: Are there any online calculators to help with this conversion?
A: While numerous online calculators can perform this conversion, understanding the underlying process is more beneficial than relying solely on calculators. This understanding will help you approach similar problems effectively.
Conclusion
Converting 3/40 to a percentage, whether using direct division, equivalent fractions, or proportions, ultimately yields the same result: 7.5%. This process isn't just about finding a numerical answer; it's about grasping the fundamental relationship between fractions and percentages, a skill applicable to a wide range of mathematical and real-world problems. Mastering this conversion strengthens your mathematical foundation and equips you to tackle more complex percentage-based calculations with confidence. Remember to practice regularly to reinforce your understanding and build proficiency.
Latest Posts
Latest Posts
-
Rotational Inertia Of A Cube
Sep 13, 2025
-
Word Problems About Pythagorean Theorem
Sep 13, 2025
-
15 3 5 Of 250
Sep 13, 2025
-
What Are Texas Natural Resources
Sep 13, 2025
-
Full Wave Vs Bridge Rectifier
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.