Gcf Of 56 And 72
salachar
Sep 08, 2025 · 6 min read
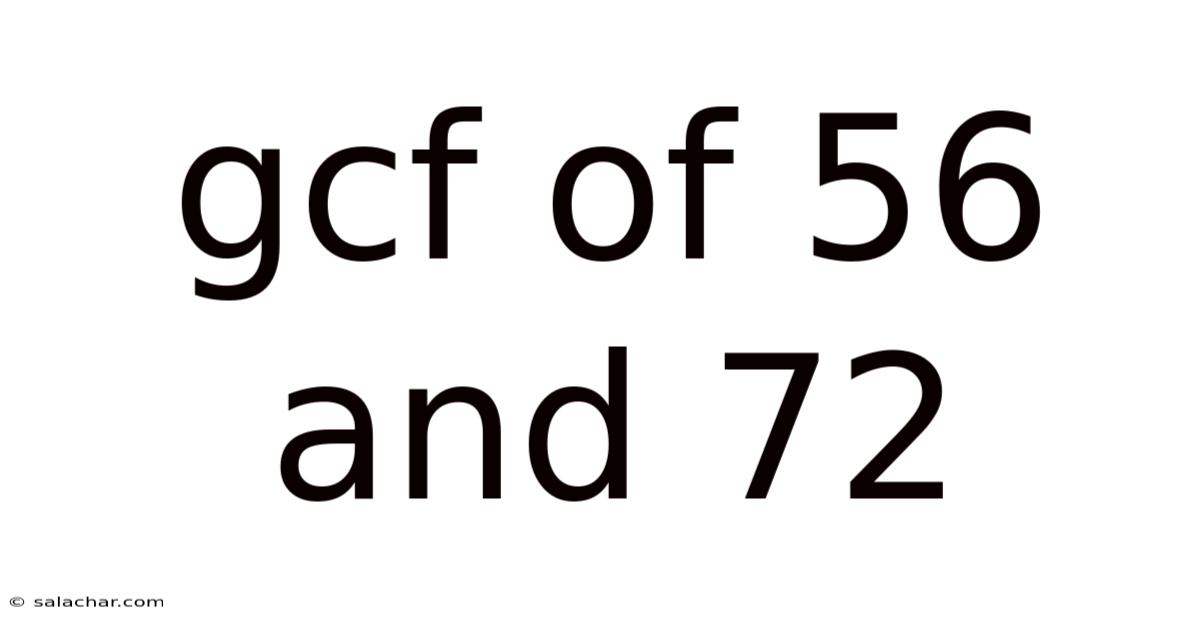
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 56 and 72: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the GCF is crucial for a deeper grasp of number theory and its applications in various fields like cryptography and computer science. This article will delve into the GCF of 56 and 72, exploring multiple approaches to solve this problem and expanding upon the broader mathematical principles involved. We will move beyond a simple answer and provide a robust understanding of this fundamental concept.
Understanding Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 56 and 72, let's define what it actually means. The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Think of it like finding the largest building block that can be used to construct both numbers.
For example, if we consider the numbers 12 and 18, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore the GCF(12, 18) = 6.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers like 56 and 72, is to list all the factors of each number and then identify the largest common factor.
Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Comparing the two lists, we see that the common factors are 1, 2, 4, and 8. The greatest of these common factors is 8.
Therefore, the GCF(56, 72) = 8.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 56:
We can break down 56 into its prime factors as follows:
56 = 2 x 28 = 2 x 2 x 14 = 2 x 2 x 2 x 7 = 2³ x 7¹
Prime Factorization of 72:
Similarly, for 72:
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Now, we identify the common prime factors: Both numbers share three factors of 2 (2³). There are no other common prime factors.
Therefore, the GCF(56, 72) = 2³ = 8.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 56 and 72:
- 72 = 1 x 56 + 16 (We subtract 56 from 72, leaving a remainder of 16)
- 56 = 3 x 16 + 8 (We subtract three times 16 from 56, leaving a remainder of 8)
- 16 = 2 x 8 + 0 (We subtract two times 8 from 16, leaving a remainder of 0)
When the remainder is 0, the GCF is the last non-zero remainder, which is 8.
Therefore, the GCF(56, 72) = 8.
Illustrative Applications of GCF
Understanding the GCF has practical applications beyond simple arithmetic exercises. Here are a few examples:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 56/72 can be simplified by dividing both the numerator and denominator by their GCF (8), resulting in the equivalent fraction 7/9.
-
Dividing Objects Evenly: Imagine you have 56 apples and 72 oranges, and you want to divide them into identical groups with the maximum number of items in each group. The GCF (8) tells you that you can create 8 identical groups, each containing 7 apples and 9 oranges.
-
Geometry Problems: GCF plays a role in solving geometry problems involving areas and dimensions. For example, finding the largest square tile that can perfectly cover a rectangular floor with dimensions 56 cm and 72 cm requires calculating the GCF of 56 and 72 (8 cm).
-
Cryptography: The concept of GCF is fundamental to many cryptographic algorithms, including the RSA algorithm, which relies heavily on prime factorization and the GCF to ensure data security.
Frequently Asked Questions (FAQ)
-
What if the GCF of two numbers is 1? If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Can I find the GCF of more than two numbers? Yes, the same methods can be extended to find the GCF of more than two numbers. For example, to find the GCF(56, 72, 84), you can find the GCF of 56 and 72 (which is 8), and then find the GCF of 8 and 84 (which is 4). Therefore, GCF(56, 72, 84) = 4.
-
Which method is the best for finding the GCF? The best method depends on the numbers involved. For small numbers, listing factors is simple. For larger numbers, the Euclidean algorithm is generally the most efficient. Prime factorization provides a good conceptual understanding.
-
What if the numbers are very large? For extremely large numbers, specialized algorithms are employed to efficiently compute the GCF, often leveraging the principles of modular arithmetic.
Conclusion
Finding the greatest common factor of 56 and 72, as demonstrated through various methods, highlights the importance of understanding fundamental mathematical concepts. While the answer – 8 – is straightforward, the journey to arrive at that answer showcases different approaches and their underlying principles. This understanding extends beyond simple arithmetic, demonstrating the relevance of GCF in various applications, from everyday problem-solving to complex mathematical fields. By mastering the concepts presented here, you will be well-equipped to tackle more complex number theory challenges and appreciate the interconnectedness of mathematical ideas. The ability to find the GCF efficiently and understand its implications is a valuable skill in both academic and practical contexts.
Latest Posts
Latest Posts
-
What Is 30 Of 2
Sep 09, 2025
-
Pv Diagram Of Isothermal Process
Sep 09, 2025
-
5 25 As A Mixed Number
Sep 09, 2025
-
Decibels Are Used To Measure
Sep 09, 2025
-
Does A Deer Eat Meat
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 56 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.