Solve 2x 3 9 X
salachar
Sep 09, 2025 · 6 min read
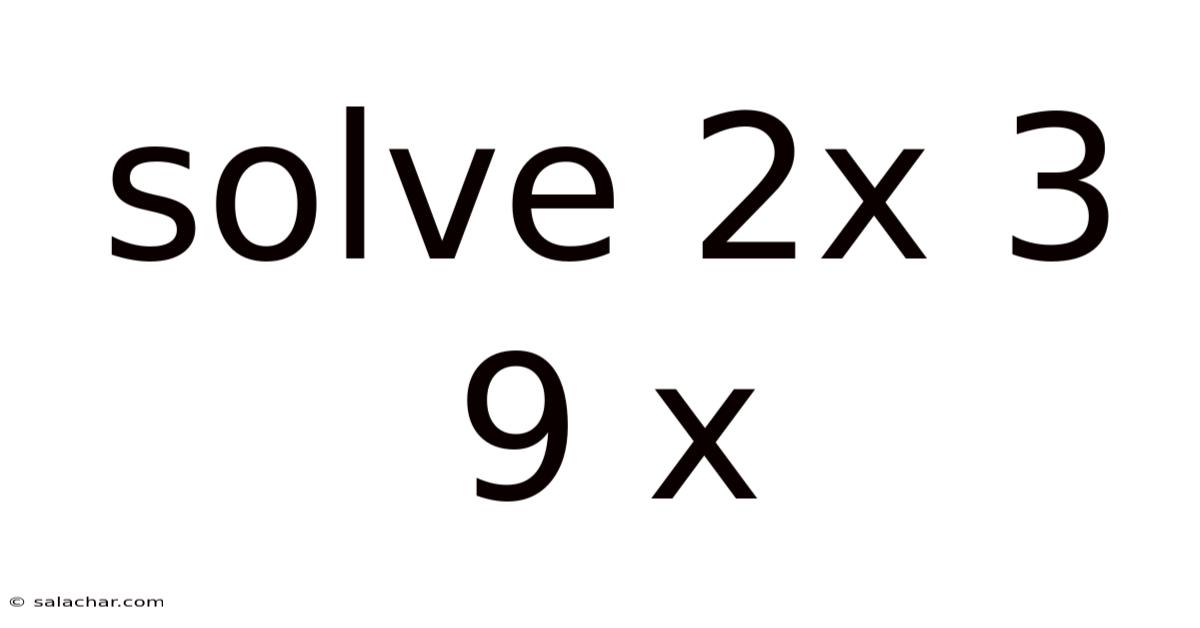
Table of Contents
Solving the Equation: 2x + 3 = 9x
This article provides a comprehensive guide on how to solve the algebraic equation 2x + 3 = 9x. We'll explore the steps involved, the underlying mathematical principles, and common mistakes to avoid. Whether you're a student brushing up on your algebra skills or simply curious about solving equations, this guide will equip you with the knowledge and confidence to tackle similar problems. Understanding this seemingly simple equation lays the groundwork for solving more complex algebraic expressions.
Introduction: Understanding the Fundamentals
Before diving into the solution, let's refresh some fundamental concepts in algebra. The equation 2x + 3 = 9x is a linear equation, meaning the highest power of the variable 'x' is 1. Solving this equation involves finding the value of 'x' that makes the equation true. This value is often referred to as the solution, root, or zero of the equation. The process relies on the principles of maintaining equality: whatever operation you perform on one side of the equation, you must perform the same operation on the other side to keep the equation balanced.
Step-by-Step Solution: Isolating the Variable
Now let's systematically solve the equation 2x + 3 = 9x. Our goal is to isolate the variable 'x' on one side of the equation. Here's a step-by-step approach:
Step 1: Gather the 'x' terms.
To begin, we want to bring all terms containing 'x' to one side of the equation. We can achieve this by subtracting 2x from both sides:
2x + 3 - 2x = 9x - 2x
This simplifies to:
3 = 7x
Step 2: Isolate 'x'.
Now, 'x' is multiplied by 7. To isolate 'x', we need to divide both sides of the equation by 7:
3/7 = 7x/7
This simplifies to:
x = 3/7
Therefore, the solution to the equation 2x + 3 = 9x is x = 3/7.
Verification: Checking the Solution
It's always a good practice to verify your solution by substituting it back into the original equation. Let's check if x = 3/7 satisfies the equation 2x + 3 = 9x:
2(3/7) + 3 = 9(3/7)
6/7 + 3 = 27/7
To add the fractions, we need a common denominator:
6/7 + 21/7 = 27/7
27/7 = 27/7
Since both sides are equal, our solution x = 3/7 is correct.
Understanding the Underlying Principles: Properties of Equality
The solution process hinges on fundamental properties of equality:
-
Subtraction Property of Equality: If a = b, then a - c = b - c. This allows us to subtract the same quantity from both sides of an equation without changing its truth value. We used this property in Step 1.
-
Division Property of Equality: If a = b and c ≠ 0, then a/c = b/c. This allows us to divide both sides of an equation by the same non-zero quantity without changing its truth value. We used this property in Step 2.
These properties, along with the addition and multiplication properties of equality, form the basis for solving a wide range of algebraic equations.
Common Mistakes and How to Avoid Them
While solving linear equations might seem straightforward, several common mistakes can lead to incorrect solutions. Let's address some of these:
-
Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) – Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Failing to follow this order can lead to incorrect simplification.
-
Errors in Sign Manipulation: Be meticulous with signs, especially when dealing with negative numbers. A simple sign error can drastically alter the solution. Double-check your work carefully.
-
Dividing by Zero: Never divide by zero. This is undefined in mathematics. If you encounter a situation where you're tempted to divide by a variable that might be zero, consider alternative approaches to solve the equation.
-
Not Verifying the Solution: Always check your answer by substituting it back into the original equation. This helps catch any errors you might have made during the solution process.
Expanding the Concept: Solving More Complex Equations
The principles used to solve 2x + 3 = 9x are applicable to more complex linear equations. For instance, consider an equation like 5x + 7 = 2x - 4. The steps would be similar:
- Gather 'x' terms: Subtract 2x from both sides: 3x + 7 = -4
- Isolate the constant term: Subtract 7 from both sides: 3x = -11
- Isolate 'x': Divide both sides by 3: x = -11/3
The same principles of equality and order of operations apply.
Real-World Applications: Where Linear Equations are Used
Linear equations have widespread applications in various fields, including:
-
Physics: Modeling motion, calculating forces, and understanding relationships between physical quantities.
-
Engineering: Designing structures, analyzing circuits, and optimizing systems.
-
Economics: Analyzing market trends, predicting demand, and modeling economic growth.
-
Finance: Calculating interest, determining investments, and forecasting financial outcomes.
Understanding how to solve linear equations is a crucial skill with far-reaching applications.
Frequently Asked Questions (FAQ)
Q1: What if the equation had more than one variable?
A1: If the equation has more than one variable (e.g., 2x + 3y = 9), you would need additional equations to solve for the values of both x and y. This would involve techniques like substitution or elimination, which are beyond the scope of this specific problem but are fundamental concepts in linear algebra.
Q2: What if the equation involved fractions?
A2: If the equation involves fractions, you can solve it by finding a common denominator for all fractions and then simplifying. Alternatively, you could multiply both sides of the equation by the least common multiple (LCM) of the denominators to eliminate the fractions before proceeding with the solution.
Q3: Can this equation be solved graphically?
A3: Yes. The equation 2x + 3 = 9x can be represented graphically as two lines: y = 2x + 3 and y = 9x. The solution to the equation is the x-coordinate of the point where these two lines intersect. Graphically solving this would show the intersection at x = 3/7.
Q4: Are there other methods to solve this type of equation?
A4: While the method presented here is the most straightforward, other methods like using matrices (for more complex systems of linear equations) exist. However, for a simple linear equation like this, the method described above is the most efficient and easily understood.
Conclusion: Mastering Linear Equations
Solving the equation 2x + 3 = 9x provides a fundamental understanding of solving linear equations. By mastering the steps involved and understanding the underlying principles, you equip yourself with a crucial skill applicable across numerous fields. Remember to always verify your solution and be meticulous in your calculations to avoid common errors. Practice solving various linear equations to build confidence and proficiency in this essential algebraic skill. The ability to manipulate equations and isolate variables is a cornerstone of mathematical problem-solving. Through consistent practice and a firm grasp of the underlying principles, you can confidently tackle more complex algebraic problems in the future.
Latest Posts
Latest Posts
-
Timber Timbre Run From Me
Sep 09, 2025
-
Square Root Of 17 Simplified
Sep 09, 2025
-
Cross Section Of Monocot Leaf
Sep 09, 2025
-
Is 23 Even Or Odd
Sep 09, 2025
-
2 Kg How Many Grams
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Solve 2x 3 9 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.