Three Decreased By A Number
salachar
Sep 15, 2025 · 5 min read
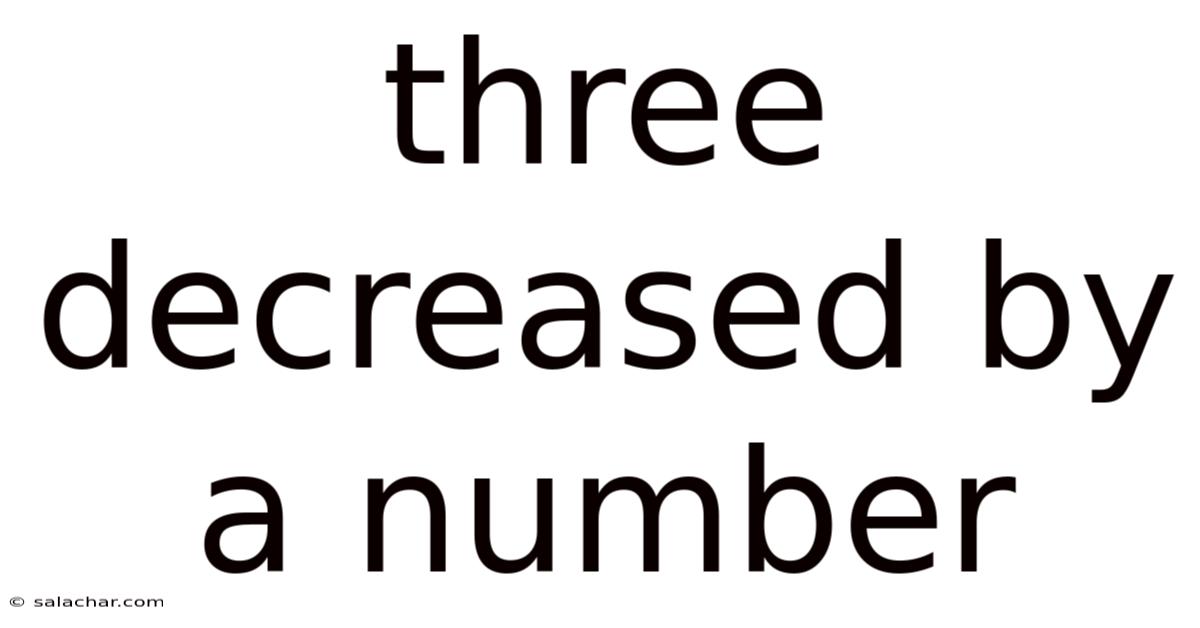
Table of Contents
Three Decreased by a Number: Exploring Subtraction and its Applications
This article delves into the seemingly simple mathematical expression, "three decreased by a number." While the concept appears basic, understanding its nuances unlocks a deeper appreciation for fundamental algebraic principles and their real-world applications. We'll explore the expression's representation, its connection to subtraction, problem-solving techniques, and how it lays the groundwork for more complex mathematical concepts. This exploration will cover various levels, making it accessible to both beginners and those seeking a refresher.
Understanding the Expression: "Three Decreased by a Number"
The phrase "three decreased by a number" directly translates to a subtraction problem. It signifies that we start with the number three and subtract an unspecified quantity, often represented by a variable (like x, y, or n). Therefore, the mathematical representation is: 3 - x (where x represents the unknown number). This simple equation forms the basis for numerous mathematical explorations and problem-solving scenarios.
Representing the Expression Algebraically
Algebra provides the tools to represent this phrase concisely and systematically. The expression "three decreased by a number" is represented as:
- 3 - n (where 'n' is the number)
This algebraic representation allows us to manipulate and solve equations involving this expression. For instance, if we know the result of "three decreased by a number," we can set up an equation to find the value of the unknown number. For example:
- 3 - n = 1 (Three decreased by a number equals one)
Solving this equation involves isolating 'n' by adding 'n' to both sides and subtracting 1 from both sides, resulting in: n = 2.
Solving Problems Involving "Three Decreased by a Number"
Let's explore different problem-solving scenarios involving this expression:
Scenario 1: Finding the Unknown Number
-
Problem: John had three apples. He gave away some apples, and he now has only one apple left. How many apples did he give away?
-
Solution: We can represent this problem using the expression "three decreased by a number." Let's use 'a' to represent the number of apples John gave away. The equation becomes: 3 - a = 1. Solving for 'a', we find that a = 2. John gave away two apples.
Scenario 2: Word Problems with Multiple Steps
-
Problem: Maria has three times as many marbles as David. If David has 'x' marbles, and Maria gives away 2 marbles, how many marbles does Maria have left?
-
Solution: This problem involves multiple steps. First, we determine the number of marbles Maria has: 3x. Then, we represent the number of marbles she has left after giving away two: 3x - 2. This expression represents "three times the number of David's marbles decreased by two."
Scenario 3: Negative Numbers
-
Problem: If "three decreased by a number" equals -1, what is the number?
-
Solution: The equation becomes: 3 - n = -1. To solve, we add 'n' to both sides and add 1 to both sides: n = 4. This illustrates that the unknown number can be greater than three, resulting in a negative outcome when subtracted from three.
Exploring the Concept of Subtraction
The expression "three decreased by a number" fundamentally revolves around the concept of subtraction. Subtraction is one of the four basic arithmetic operations, involving the removal of a quantity from another. Understanding its properties is crucial:
-
Commutative Property: Subtraction is not commutative. This means that the order of the numbers matters. 3 - 2 is not the same as 2 - 3.
-
Associative Property: Subtraction is not associative. (3 - 2) - 1 is not the same as 3 - (2 - 1).
-
Identity Property: Subtracting zero from a number does not change the number's value. 3 - 0 = 3.
-
Inverse Property: Adding a number and then subtracting the same number results in the original number. 3 + 2 - 2 = 3.
Connecting to More Advanced Concepts
The seemingly simple expression "three decreased by a number" serves as a stepping stone to more complex mathematical concepts:
-
Functions: The expression can be considered a simple function where the input is the number (x) and the output is the result of the subtraction (3 - x).
-
Linear Equations: When we set "three decreased by a number" equal to another value, we create a linear equation. Solving these equations is a fundamental skill in algebra.
-
Inequalities: We can extend this to inequalities, such as "three decreased by a number is greater than one" (3 - x > 1). Solving these inequalities involves similar techniques but with considerations for the inequality symbols.
-
Graphing: The expression can be graphed as a line on a coordinate plane. This visual representation helps in understanding the relationship between the input (x) and the output (3 - x).
Frequently Asked Questions (FAQ)
Q1: Can the number be zero?
A1: Yes, absolutely. If the number is zero, the expression becomes 3 - 0 = 3.
Q2: Can the number be negative?
A2: Yes, the number can be negative. For example, if the number is -2, the expression becomes 3 - (-2) = 5. Remember that subtracting a negative number is the same as adding its positive counterpart.
Q3: What if the result of "three decreased by a number" is negative?
A3: A negative result simply means that the number subtracted from three is greater than three. For example, if 3 - x = -2, then x = 5.
Q4: How does this relate to real-world problems?
A4: This concept is applicable in numerous situations. Think about calculating remaining quantities, determining differences in values, or solving problems involving profit and loss. It's a foundational concept in various fields.
Conclusion: The Significance of Simplicity
The expression "three decreased by a number" might seem trivial at first glance. However, its simplicity belies its significance. Understanding this seemingly basic concept lays a strong foundation for grasping more complex mathematical ideas. By exploring its algebraic representation, solving various problem types, and connecting it to broader mathematical concepts, we gain a deeper appreciation for the power and versatility of even the most fundamental mathematical operations. This understanding is crucial for building a strong mathematical foundation and applying these principles to solve real-world problems. The journey from a simple phrase to a comprehensive understanding of algebraic principles highlights the beauty and power of mathematical reasoning. Mastering this fundamental concept opens doors to a wider understanding of more advanced mathematical topics and their diverse applications.
Latest Posts
Latest Posts
-
The West Is The Best
Sep 15, 2025
-
What Is 25 Of 96
Sep 15, 2025
-
Effect Of Temperature On Solubility
Sep 15, 2025
-
Electron Dot Formula Of Carbon
Sep 15, 2025
-
Onion Cell Under Microscope 40x
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Three Decreased By A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.