What Is 75 Of 11
salachar
Sep 14, 2025 · 5 min read
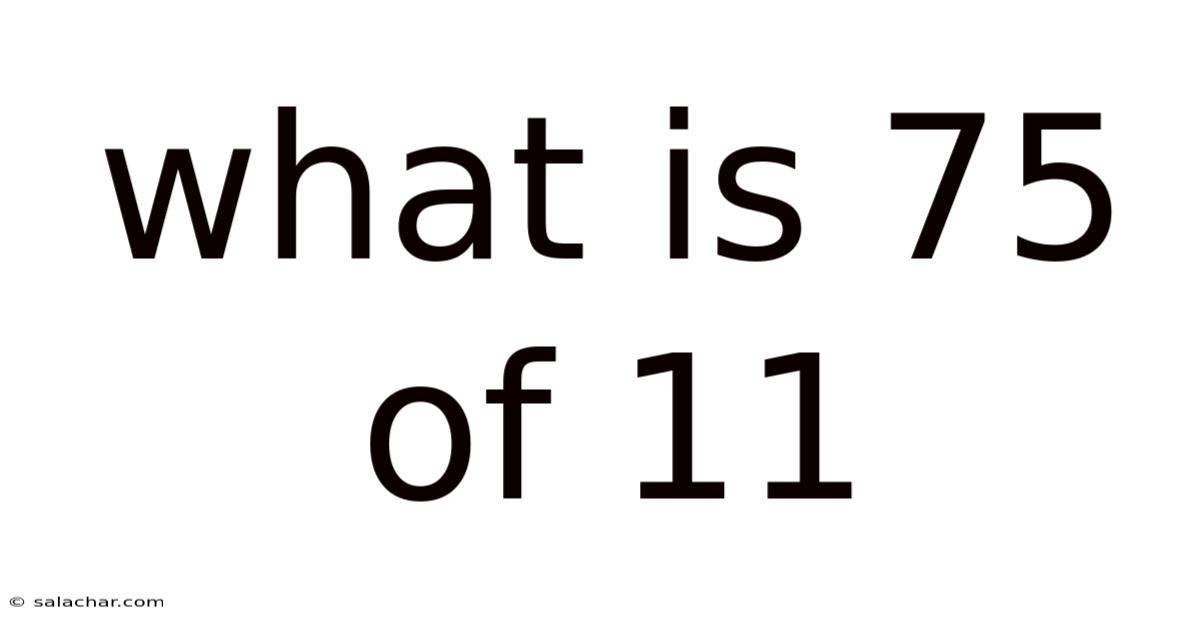
Table of Contents
What is 75% of 11? A Deep Dive into Percentages and Their Applications
Finding 75% of 11 might seem like a simple calculation, but it opens the door to understanding a fundamental mathematical concept: percentages. This article will not only solve this specific problem but also explore the broader meaning of percentages, different methods for calculating them, and their widespread applications in everyday life, from budgeting and shopping to scientific research and financial analysis. We'll delve into the intricacies of percentage calculations, providing a comprehensive understanding for learners of all levels.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio where the denominator is always 100. The symbol "%" represents "percent," which means "out of 100." So, 75% literally means 75 out of 100, or 75/100. This fraction can be simplified to 3/4. Understanding this fundamental concept is crucial before tackling any percentage calculation.
Method 1: Converting Percentage to Decimal
The most common method for calculating a percentage of a number involves converting the percentage to a decimal. To do this, divide the percentage by 100.
-
Step 1: Convert 75% to a decimal: 75% ÷ 100 = 0.75
-
Step 2: Multiply the decimal by the number: 0.75 x 11 = 8.25
Therefore, 75% of 11 is 8.25.
Method 2: Using Fractions
As mentioned earlier, 75% can be expressed as the fraction 3/4. This method provides an alternative approach:
-
Step 1: Express the percentage as a fraction: 75% = 3/4
-
Step 2: Multiply the fraction by the number: (3/4) x 11 = 33/4
-
Step 3: Convert the improper fraction to a decimal: 33/4 = 8.25
Again, we arrive at the answer: 75% of 11 is 8.25.
Method 3: Proportion Method
The proportion method utilizes the concept of equivalent ratios. We set up a proportion to solve for the unknown value.
-
Step 1: Set up a proportion: 75/100 = x/11 (where 'x' represents 75% of 11)
-
Step 2: Cross-multiply: 75 * 11 = 100 * x
-
Step 3: Solve for x: 825 = 100x => x = 825/100 = 8.25
This confirms that 75% of 11 is 8.25.
Why Different Methods? Understanding the Flexibility of Percentage Calculations
While all three methods yield the same result, understanding each approach offers flexibility depending on the context and personal preference. The decimal method is often the quickest and most straightforward, especially for simple calculations. The fraction method is beneficial when dealing with easily convertible percentages like 25%, 50%, or 75%. The proportion method is valuable for understanding the underlying principle of equivalent ratios and can be adapted to more complex percentage problems.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life. Here are a few examples:
-
Shopping and Sales: Discounts are often expressed as percentages. Calculating the final price after a 20% discount requires understanding percentage calculations.
-
Finance and Investments: Interest rates on loans and savings accounts are expressed as percentages. Calculating the interest earned or paid necessitates proficiency in percentage calculations.
-
Taxes: Sales tax, income tax, and property tax are calculated as percentages of the taxable amount. Understanding these calculations is crucial for financial planning.
-
Science and Statistics: Percentages are frequently used to represent data in scientific studies, statistical analyses, and research reports. Interpreting these results requires a sound understanding of percentage calculations.
-
Data Representation: Charts and graphs often use percentages to visually represent proportions and trends within a dataset, making data analysis more intuitive and accessible.
-
Grading and Assessment: Many educational systems use percentages to represent student performance on tests and assignments. Understanding percentages is crucial for students to monitor their progress and academic standing.
-
Cooking and Baking: Recipes often specify ingredient quantities as percentages of the total weight or volume, especially in professional baking and pastry-making, for precise results.
Beyond the Basics: More Complex Percentage Problems
While finding 75% of 11 is a relatively simple calculation, the principles extend to more complex problems involving:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, what percentage of 20 is 5? (Answer: 25%)
-
Finding the whole: If you know the part and the percentage, you can find the whole. For example, if 20% of a number is 10, what is the number? (Answer: 50)
-
Percentage increase and decrease: These calculations involve finding the percentage change between two values. For example, calculating the percentage increase in price from $10 to $15, or the percentage decrease in sales from 100 units to 80 units.
-
Compound interest: This involves calculating interest on both the principal and accumulated interest over time, requiring iterative percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a different percentage of 11?
- A: Use the same methods outlined above, substituting the desired percentage for 75%. Simply convert the new percentage to a decimal or fraction and multiply it by 11.
-
Q: Can I use a calculator for percentage calculations?
- A: Absolutely! Calculators greatly simplify percentage calculations, especially for more complex problems. Most calculators have a percentage function (%) that streamlines the process.
-
Q: Are there online percentage calculators?
- A: Yes, many websites offer free online percentage calculators. These can be helpful for double-checking calculations or for solving more intricate percentage problems.
-
Q: Why is understanding percentages important?
- A: Percentages are fundamental to numerous aspects of life, from personal finance to professional fields. A strong grasp of percentage calculations empowers you to make informed decisions, interpret data effectively, and navigate various quantitative scenarios.
Conclusion: Mastering the Art of Percentages
This in-depth exploration of percentage calculations, particularly focusing on finding 75% of 11, highlights the importance of this fundamental mathematical concept. Understanding different methods for calculating percentages, along with their diverse applications, provides a valuable skill applicable in various contexts. From everyday shopping to advanced financial analysis, mastering percentages enhances your ability to solve problems, interpret data, and make informed decisions in a world increasingly reliant on numerical understanding. Remember, while the specific calculation of 75% of 11 yields a simple answer (8.25), the broader principles and applications of percentages are far-reaching and essential for navigating the complexities of the modern world. Practice makes perfect, so keep working with various percentage problems to build your confidence and proficiency.
Latest Posts
Latest Posts
-
3 Times What Equals 72
Sep 14, 2025
-
Red Vs White Muscle Fibers
Sep 14, 2025
-
Is 35 A Perfect Square
Sep 14, 2025
-
Which Tools Would You Use
Sep 14, 2025
-
Carboxylic Acid To An Aldehyde
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.