X 2 3 2x 1
salachar
Sep 08, 2025 · 6 min read
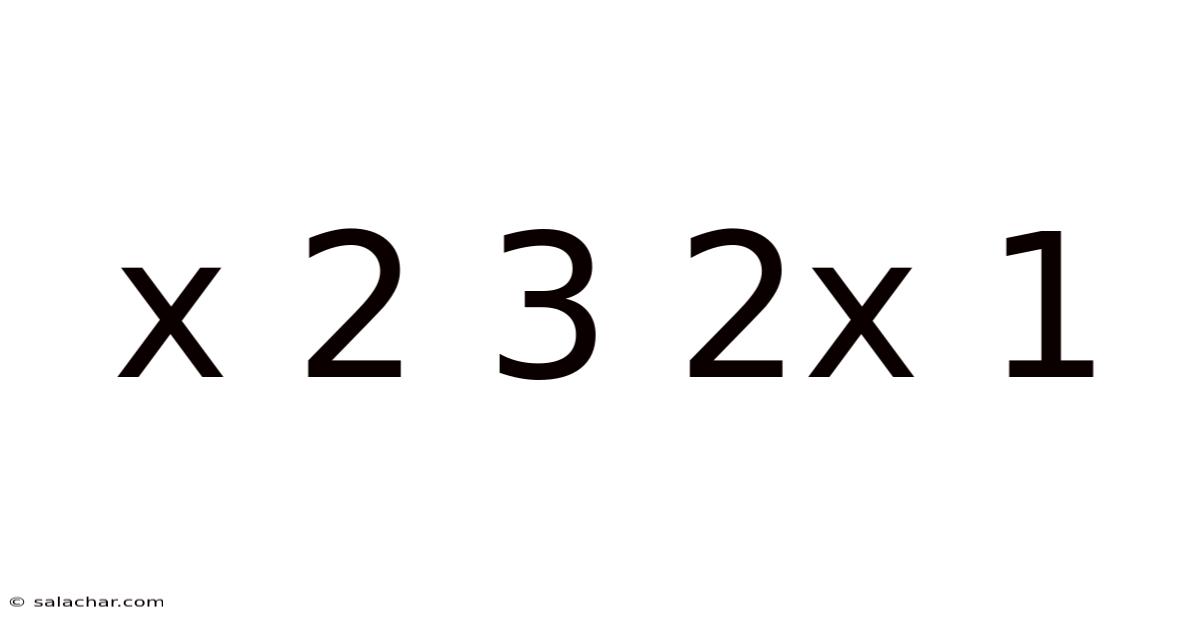
Table of Contents
Exploring the Mathematical Expression: x² + 3x + 2x + 1
This article delves into the mathematical expression x² + 3x + 2x + 1, exploring its simplification, solving methods, applications, and underlying concepts. We'll cover everything from basic algebraic manipulation to more advanced techniques, ensuring a comprehensive understanding for students and enthusiasts alike. Understanding this seemingly simple expression provides a strong foundation for more complex algebraic concepts. This guide will equip you with the tools to confidently tackle similar problems and appreciate the elegance of mathematical reasoning.
Introduction: Understanding the Components
The expression x² + 3x + 2x + 1 is a polynomial, specifically a quadratic expression. Let's break down its components:
- x²: This term represents x squared, or x multiplied by itself (x * x). It's a quadratic term, the highest power of x in the expression.
- 3x and 2x: These are linear terms. They represent x multiplied by a constant (3 and 2 respectively).
- 1: This is the constant term, a numerical value independent of x.
Understanding these individual components is crucial before attempting to simplify or solve the expression.
Simplifying the Expression
The first step in working with this expression is simplification. We can combine like terms to make the expression more manageable. Like terms are terms that have the same variable raised to the same power. In this case, 3x and 2x are like terms. Combining them, we get:
x² + 3x + 2x + 1 = x² + 5x + 1
This simplified form is much easier to work with for further analysis or problem-solving.
Solving for x: Finding the Roots
Solving for x means finding the values of x that make the expression equal to zero. This involves finding the roots or zeros of the quadratic equation:
x² + 5x + 1 = 0
This equation cannot be easily factored, so we need to use other methods to find the solutions for x. Two common methods are:
- Quadratic Formula: This formula provides a direct solution for any quadratic equation in the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our equation, a = 1, b = 5, and c = 1. Substituting these values into the quadratic formula gives:
x = [-5 ± √(5² - 4 * 1 * 1)] / 2 * 1 x = [-5 ± √(21)] / 2
This gives us two solutions:
x₁ = (-5 + √21) / 2 x₂ = (-5 - √21) / 2
These are the roots of the quadratic equation. They represent the points where the graph of the quadratic function intersects the x-axis.
- Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. The steps are as follows:
- Move the constant term to the right side: x² + 5x = -1
- Take half of the coefficient of the linear term (5), square it (25/4), and add it to both sides: x² + 5x + 25/4 = -1 + 25/4
- Factor the left side as a perfect square: (x + 5/2)² = 21/4
- Take the square root of both sides: x + 5/2 = ±√(21/4)
- Solve for x: x = -5/2 ± √21/2
This gives the same solutions as the quadratic formula.
Graphical Representation
The equation x² + 5x + 1 = 0 can be represented graphically as a parabola. The parabola opens upwards because the coefficient of the x² term is positive. The x-intercepts of the parabola represent the roots of the equation, which we calculated above using the quadratic formula and completing the square. The y-intercept is found by setting x = 0, which gives y = 1.
Applications of Quadratic Equations
Quadratic equations have numerous applications in various fields, including:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing bridges, buildings, and other structures; optimizing shapes and materials for maximum strength and efficiency.
- Economics: Modeling supply and demand curves, calculating profit and loss.
- Computer Science: Used in algorithms and data structures.
The ability to solve quadratic equations is therefore essential for many scientific and engineering disciplines.
Expanding on the Concept: Factoring and the Distributive Property
Before we simplified the original expression, we had x² + 3x + 2x + 1. This expression could also be approached by factoring. While not directly applicable to solving for x in this case, understanding factoring is crucial for other quadratic equations. Let's examine a similar expression that can be factored:
x² + 5x + 6 = 0
This equation can be factored as:
(x + 2)(x + 3) = 0
This factored form reveals the roots immediately: x = -2 and x = -3. This illustrates the relationship between the roots and the factors of a quadratic equation. The distributive property (also known as the FOIL method – First, Outer, Inner, Last) allows us to expand factored expressions to their polynomial form:
(x + 2)(x + 3) = x² + 3x + 2x + 6 = x² + 5x + 6
This demonstrates the reversibility between factored and expanded forms.
Further Exploration: Discriminant and Nature of Roots
The discriminant, represented by Δ (Delta), is the expression inside the square root in the quadratic formula (b² - 4ac). The discriminant tells us about the nature of the roots:
- Δ > 0: The equation has two distinct real roots.
- Δ = 0: The equation has one real root (a repeated root).
- Δ < 0: The equation has two complex roots (involving imaginary numbers).
In our original equation, x² + 5x + 1 = 0, the discriminant is:
Δ = 5² - 4 * 1 * 1 = 21
Since Δ > 0, the equation has two distinct real roots, as we calculated earlier.
Frequently Asked Questions (FAQ)
- Q: What if the expression was x² + 3x – 2x + 1?
A: In this case, the linear terms would simplify to x (3x – 2x = x), resulting in the expression x² + x + 1 = 0. This equation would also be solved using the quadratic formula or completing the square.
- Q: Can all quadratic equations be factored easily?
A: No, many quadratic equations cannot be easily factored and require the quadratic formula or completing the square for solving.
- Q: What is the difference between a quadratic equation and a quadratic expression?
A: A quadratic expression is a mathematical phrase containing a variable raised to the power of two, along with other terms potentially including the variable raised to the power of one and a constant term. A quadratic equation is a statement that sets a quadratic expression equal to zero. The goal with a quadratic equation is to find the values of the variable that make the equation true.
- Q: Why is understanding quadratic equations important?
A: Quadratic equations are fundamental to many areas of mathematics and its applications in science and engineering. They model many real-world phenomena and are crucial for solving various problems.
Conclusion: Mastering the Fundamentals
This in-depth exploration of the seemingly simple expression x² + 3x + 2x + 1 has demonstrated the rich mathematical concepts underlying it. From simplifying the expression to solving for x using various methods, analyzing its graphical representation, and understanding its broader applications, we've covered a significant portion of fundamental algebra. Mastering these concepts forms a solid foundation for tackling more advanced mathematical challenges and provides valuable tools for various fields of study and real-world problem-solving. Remember that consistent practice and a thorough understanding of the underlying principles are key to success in algebra and beyond.
Latest Posts
Latest Posts
-
What Is 30 Of 2
Sep 09, 2025
-
Pv Diagram Of Isothermal Process
Sep 09, 2025
-
5 25 As A Mixed Number
Sep 09, 2025
-
Decibels Are Used To Measure
Sep 09, 2025
-
Does A Deer Eat Meat
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about X 2 3 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.