Root 3 Times Root 2
salachar
Sep 11, 2025 · 5 min read
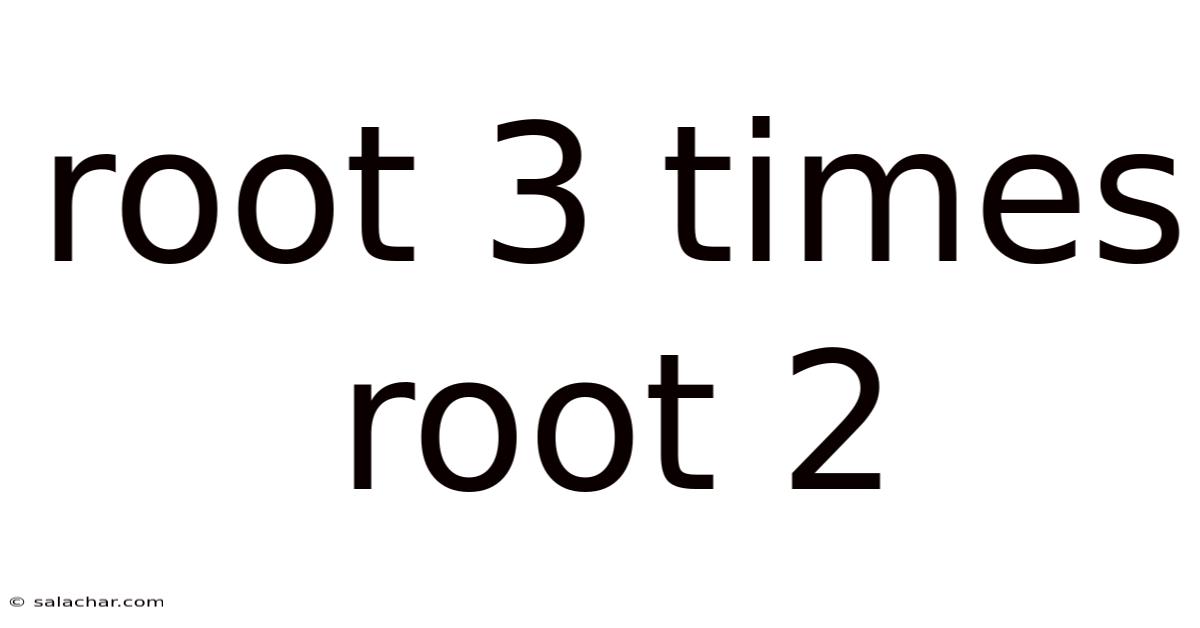
Table of Contents
Unveiling the Mystery: A Deep Dive into √3 x √2
Understanding the multiplication of surds, specifically √3 x √2, is a fundamental concept in mathematics, crucial for progressing in algebra, trigonometry, and calculus. This seemingly simple calculation opens doors to a deeper understanding of irrational numbers and their properties. This comprehensive guide will not only explain how to solve √3 x √2 but also delve into the underlying mathematical principles, explore related concepts, and address frequently asked questions. Let's unravel the mystery together!
Introduction: Understanding Surds and Their Multiplication
A surd is a radical expression that cannot be simplified to a rational number (a number that can be expressed as a fraction p/q, where p and q are integers, and q ≠ 0). Examples of surds include √2, √3, √5, and so on. These numbers are irrational, meaning their decimal representation continues infinitely without repeating. Multiplying surds involves manipulating these irrational numbers to obtain a simplified, albeit often still irrational, result.
The key to multiplying surds like √3 x √2 lies in understanding the properties of square roots. Recall that √a x √b = √(a x b) provided a and b are non-negative. This property allows us to simplify the multiplication of surds.
Calculating √3 x √2: A Step-by-Step Approach
The calculation of √3 x √2 is straightforward, applying the aforementioned property of square roots:
-
Apply the multiplication rule: √3 x √2 = √(3 x 2)
-
Perform the multiplication within the square root: √(3 x 2) = √6
Therefore, √3 x √2 = √6. While √6 is still a surd (an irrational number), it represents the simplified form of the initial expression. We cannot simplify √6 further because 6 has no perfect square factors other than 1.
Expanding the Concept: Multiplying More Complex Surds
Let's extend our understanding beyond this basic example. Consider multiplying surds with coefficients:
Example 1: 2√3 x 3√2
-
Multiply the coefficients: 2 x 3 = 6
-
Multiply the surds: √3 x √2 = √6
-
Combine the results: 6√6
Therefore, 2√3 x 3√2 = 6√6.
Example 2: (√5 + 2)(√5 - 3)
This example demonstrates multiplying expressions containing surds. We use the distributive property (also known as the FOIL method):
-
First: √5 x √5 = 5
-
Outer: √5 x (-3) = -3√5
-
Inner: 2 x √5 = 2√5
-
Last: 2 x (-3) = -6
-
Combine like terms: 5 - 3√5 + 2√5 - 6 = -1 - √5
Therefore, (√5 + 2)(√5 - 3) = -1 - √5.
The Mathematical Rationale: Properties of Radicals
The ability to multiply surds relies on the fundamental properties of radicals (square roots, cube roots, etc.):
-
Product Property: √a x √b = √(a x b) This is the cornerstone of surd multiplication, allowing us to combine the radicands (the numbers inside the square root). It's important to remember that this property applies only when a and b are non-negative.
-
Quotient Property: √(a/b) = √a / √b (where b ≠ 0). This property allows us to simplify surds involving fractions.
-
Power Property: (√a)^n = √(a^n). This property helps us deal with surds raised to powers.
Applications of Surd Multiplication in Higher Mathematics
Understanding surd multiplication isn't just an exercise in simplification. It's a building block for many advanced mathematical concepts:
-
Trigonometry: Trigonometric functions often involve surds. Calculating the lengths of sides in triangles, especially right-angled triangles, frequently leads to expressions involving surds. Simplifying these expressions often requires surd multiplication.
-
Calculus: Derivatives and integrals of functions may involve surds. Manipulating and simplifying these expressions often requires a solid understanding of surd operations.
-
Algebra: Solving quadratic equations, simplifying algebraic expressions, and working with complex numbers often involve manipulating expressions with surds.
-
Coordinate Geometry: Determining distances and slopes in coordinate geometry can result in calculations that involve surds.
Frequently Asked Questions (FAQ)
Q1: Can all surds be simplified?
A1: No. While some surds can be simplified by factoring out perfect squares (e.g., √12 = √(4 x 3) = 2√3), many cannot be simplified further. √6, for example, remains √6.
Q2: What if I have different roots (cube roots, fourth roots, etc.)?
A2: The product property doesn't directly apply to roots of different orders. For example, you can't directly multiply a square root and a cube root. Special techniques are needed to deal with such situations.
Q3: Are there any common mistakes to avoid when multiplying surds?
A3: A common mistake is incorrectly applying the product property to negative numbers. The product property √a x √b = √(a x b) is valid only when a and b are non-negative. Also, forgetting to simplify the final answer after multiplication is another frequent error.
Q4: How can I improve my proficiency in surd multiplication?
A4: Practice is key. Work through numerous examples, starting with simple ones and gradually increasing complexity. Focus on mastering the fundamental properties of radicals and applying them consistently.
Conclusion: Mastering Surds – A Foundation for Mathematical Success
Understanding surd multiplication, as demonstrated through the example of √3 x √2, is crucial for anyone pursuing advanced studies in mathematics. It’s not merely about calculating a numerical result but about grasping the fundamental properties of irrational numbers and their manipulations within algebraic expressions. By mastering this seemingly simple concept, you lay a solid foundation for tackling more complex mathematical problems across various disciplines. Regular practice and a clear understanding of the underlying principles will equip you with the confidence to tackle any surd multiplication challenge. Remember to always check your work and ensure that your answer is in the simplest form. Through consistent effort and practice, conquering the world of surds becomes an achievable goal.
Latest Posts
Latest Posts
-
What Do Pet Lizards Eat
Sep 11, 2025
-
X 2 6x 27 0
Sep 11, 2025
-
Kindergarten Words Starting With A
Sep 11, 2025
-
Fruits Starting With Letter O
Sep 11, 2025
-
0 4 Repeated As A Fraction
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Root 3 Times Root 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.